
Công thức tính chu vi và diện tích hình bình hành
Hình bình hành là một tứ giác có hai cặp cạnh đối diện song song với nhau. Hình bình hành có nhiều tính chất đặc biệt, trong đó có công thức tính chu vi và diện tích.
Công thức tính chu vi hình bình hành
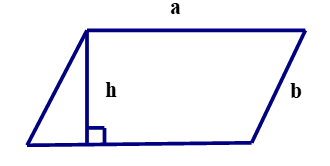
Công thức:
$$C=2.(a+b)$$
Trong đó:
- C là chu vi hình bình hành
- a là độ dài cạnh đáy hình bình hành
- b là độ dài cạnh bên hình bình hành
Ví dụ: Một hình bình hành có độ dài cạnh đáy là 5cm, độ dài cạnh bên là 3cm. Tính chu vi hình bình hành đó.
Giải:
Áp dụng công thức tính chu vi hình bình hành, ta có:
$$C=2.(a+b)=2.(5+3)=2.8=16(cm)$$
Vậy chu vi hình bình hành đó là 16cm.
Bảng tóm tắt công thức tính chu vi hình bình hành
| Công thức | Mô tả |
|---|---|
| $$C=2.(a+b)$$ | Chu vi hình bình hành |
| $$a$$ | Độ dài cạnh đáy hình bình hành |
| $$b$$ | Độ dài cạnh bên hình bình hành |
Lưu ý khi sử dụng công thức tính chu vi hình bình hành
- Công thức tính chu vi hình bình hành chỉ áp dụng cho các hình bình hành có hai cặp cạnh đối diện song song với nhau.
- Khi áp dụng công thức tính chu vi hình bình hành, cần chú ý đến đơn vị đo của các cạnh.
Công thức tính diện tích hình bình hành
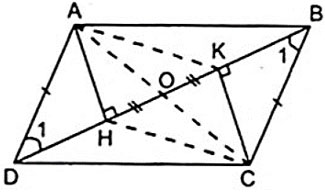
Công thức:
$$S=a.h$$
Trong đó:
- S là diện tích hình bình hành
- a là độ dài cạnh đáy hình bình hành
- h là độ dài đường cao hình bình hành
Ví dụ: Một hình bình hành có độ dài cạnh đáy là 5cm, độ dài đường cao là 3cm. Tính diện tích hình bình hành đó.
Giải:
Áp dụng công thức tính diện tích hình bình hành, ta có:
$$S=a.h=5.3=15(cm^2)$$
Vậy diện tích hình bình hành đó là 15cm^2.
Bảng tóm tắt công thức tính diện tích hình bình hành
| Công thức | Mô tả |
|---|---|
| $$S=a.h$$ | Diện tích hình bình hành |
| $$a$$ | Độ dài cạnh đáy hình bình hành |
| $$h$$ | Độ dài đường cao hình bình hành |
Lưu ý khi sử dụng công thức tính diện tích hình bình hành
- Công thức tính diện tích hình bình hành chỉ áp dụng cho các hình bình hành có hai cặp cạnh đối diện song song với nhau.
- Khi áp dụng công thức tính diện tích hình bình hành, cần chú ý đến đơn vị đo của các cạnh và đường cao.
Định lý về hình bình hành
Có nhiều định lý về hình bình hành, trong đó có 2 định lý sau:
- Định lý 1: Tổng hai cạnh đối diện của hình bình hành bằng nhau.
- Định lý 2: Hai đường chéo của hình bình hành cắt nhau tại trung điểm của mỗi đường.
Ứng dụng của định lý về hình bình hành
Định lý về hình bình hành có nhiều ứng dụng trong thực tế, chẳng hạn như:
- Tính độ dài đường chéo của hình bình hành.
- Tính diện tích hình bình hành.
- Chia hình bình hành thành các hình tam giác bằng nhau.
- Xác định tâm đối xứng của hình bình hành.
Cách áp dụng công thức tính chu vi và diện tích hình bình hành
Để áp dụng công thức tính chu vi và diện tích hình bình hành, bạn cần xác định được độ dài các cạnh và độ dài đường cao của hình bình hành đó.
Các bước áp dụng công thức tính chu vi hình bình hành
- Xác định độ dài cạnh đáy hình bình hành.
- Xác định độ dài cạnh bên hình bình hành.
- Áp dụng công thức tính chu vi hình bình hành: $$C=2.(a+b)$$.
Các bước áp dụng công thức tính diện tích hình bình hành
- Xác định độ dài cạnh đáy hình bình hành.
- Xác định độ dài đường cao hình bình hành.
- Áp dụng công thức tính diện tích hình bình hành: $$S=a.h$$.
Ví dụ minh họa về cách tính chu vi và diện tích hình bình hành
Ví dụ 1: Một hình bình hành có độ dài cạnh đáy là 5cm, độ dài cạnh bên là 3cm. Tính chu vi và diện tích hình bình hành đó.
Giải:
- Xác định độ dài cạnh đáy hình bình hành: $$a=5cm$$.
- Xác định độ dài cạnh bên hình bình hành: $$b=3cm$$.
- Áp dụng công thức tính chu vi hình bình hành: $$C=2.(a+b)=2.(5+3)=2.8=16(cm)$$.
- Áp dụng công thức tính diện tích hình bình hành: $$S=a.h=5.3=15(cm^2)$$.
Vậy chu vi hình bình hành đó là 16cm và diện tích hình bình hành đó là 15cm^2.
Ví dụ 2: Một hình bình hành có chu vi là 20cm, độ dài cạnh đáy là 6cm. Tính độ dài cạnh bên và diện tích hình bình hành đó.
Giải:
- Xác định độ dài cạnh đáy hình bình hành: $$a=6cm$$.
- Áp dụng công thức tính chu vi hình bình hành: $$C=2.(a+b) \Rightarrow 20=2.(6+b) \Rightarrow b=4(cm)$$.
- Áp dụng công thức tính diện tích hình bình hành: $$S=a.h=6.4=24(cm^2)$$.
Vậy độ dài cạnh bên hình bình hành đó là 4cm và diện tích hình bình hành đó là 24cm^2.
Bài toán liên quan đến tính chu vi và diện tích hình bình hành
- Một hình bình hành có chu vi là 40cm, độ dài cạnh đáy là 10cm. Tính độ dài cạnh bên và diện tích hình bình hành đó.
- Một hình bình hành có diện tích là 24cm^2, độ dài cạnh đáy là 6cm. Tính độ dài đường cao và chu vi hình bình hành đó.
- Một hình bình hành có độ dài cạnh đáy là 5cm, độ dài đường cao là 3cm. Tính chu vi và diện tích hình bình hành đó.
Ứng dụng của công thức tính chu vi và diện tích hình bình hành trong thực tế
Công thức tính chu vi và diện tích hình bình hành có nhiều ứng dụng trong thực tế, chẳng hạn như:
- Tính toán diện tích sàn nhà, tường nhà, trần nhà.
- Tính toán diện tích đất xây nhà, xây ao, xây hồ.
- Tính toán diện tích ruộng lúa, vườn cây, ao cá.
- Tính toán diện tích vải may quần áo, chăn màn, rèm cửa.
Lịch sử hình thành công thức tính chu vi và diện tích hình bình hành
Công thức tính chu vi và diện tích hình bình hành được hình thành từ thời cổ đại. Các nhà toán học Hy Lạp cổ đại, chẳng hạn như Thales và Pythagoras, đã nghiên cứu và phát triển các công thức này. Công thức tính chu vi và diện tích hình bình hành được sử dụng rộng rãi trong toán học và nhiều lĩnh vực khác.
Những lưu ý khi sử dụng công thức tính chu vi và diện tích hình bình hành
Khi sử dụng công thức tính chu vi và diện tích hình bình hành, cần lưu ý một số điều sau:
- Đảm bảo rằng hình đó là hình bình hành thực sự, tức là có hai cặp cạnh đối diện song song với nhau.
- Đơn vị đo của các cạnh và đường cao phải thống nhất.
- Kiểm tra lại kết quả tính toán để đảm bảo tính chính xác.
Tài liệu tham khảo về công thức tính chu vi và diện tích hình bình hành
- Sách giáo khoa Toán lớp 7, 8, 9.
- Tài liệu hướng dẫn tính toán diện tích hình bình hành.
- Các trang web về toán học.
Kết luận
Công thức tính chu vi và diện tích hình bình hành là những công thức cơ bản và quan trọng trong toán học. Công thức này được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về công thức tính chu vi và diện tích hình bình hành. Hãy thường xuyên luyện tập và áp dụng công thức này để nâng cao kỹ năng tính toán của mình.
Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!
Link nội dung: https://luathoanhut.vn/cong-thuc-tinh-chu-vi-va-dien-tich-hinh-binh-hanh-a23544.html