
Công thức tính chu vi hình tam giác
Chu vi hình tam giác là tổng độ dài các cạnh của hình tam giác đó. Bài viết này sẽ cung cấp cho bạn các công thức tính chu vi hình tam giác trong các trường hợp khác nhau, bao gồm tam giác thường, tam giác vuông, tam giác đều và tam giác cân.
Công thức tính chu vi hình tam giác thường
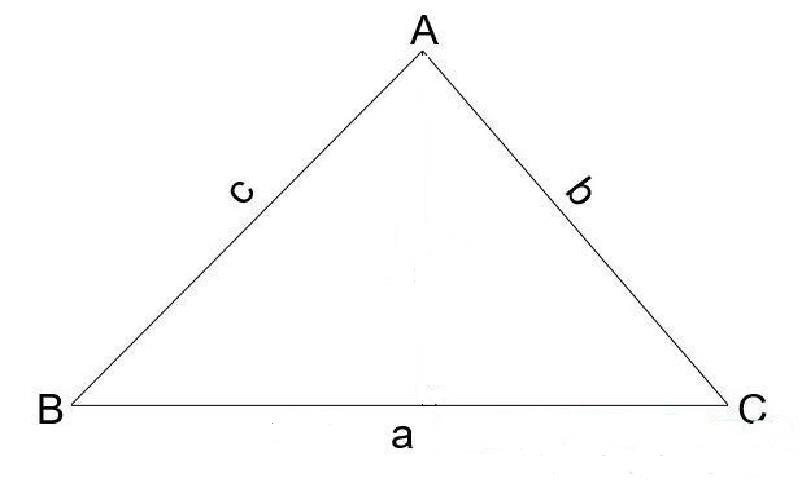
Công thức:
P = a + b + c
Trong đó:
- P là chu vi hình tam giác (đơn vị đo: cm, m, km,...)
- a, b, c là độ dài ba cạnh của hình tam giác (đơn vị đo: cm, m, km,...)
Ví dụ:
Một hình tam giác có ba cạnh lần lượt là 3cm, 4cm và 5cm. Chu vi hình tam giác đó là:
P = 3cm + 4cm + 5cm = 12cm
Công thức tính chu vi hình tam giác vuông
![]()
Trong trường hợp hình tam giác vuông, công thức tính chu vi có sự thay đổi do có một cạnh là cạnh huyền (cạnh đối diện với góc vuông).
Công thức:
P = a + b + √(a² + b²)
Trong đó:
- P là chu vi hình tam giác (đơn vị đo: cm, m, km,...)
- a, b là độ dài hai cạnh góc vuông của hình tam giác (đơn vị đo: cm, m, km,...)
Ví dụ:
Một hình tam giác vuông có hai cạnh góc vuông lần lượt là 3cm và 4cm. Chu vi hình tam giác vuông đó là:
P = 3cm + 4cm + √(3² + 4²) = 3cm + 4cm + 5cm = 12cm
Công thức tính chu vi hình tam giác đều
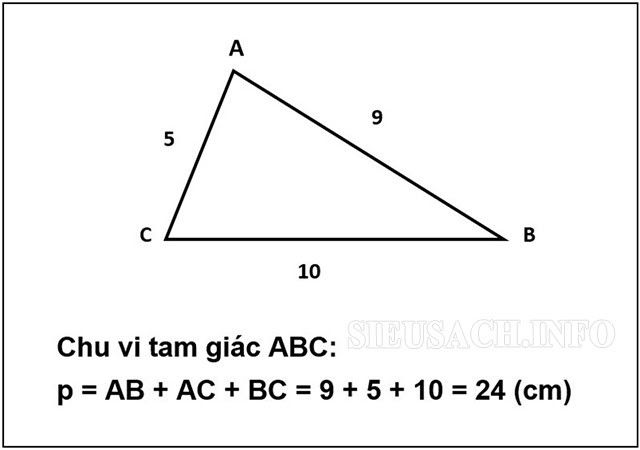
Hình tam giác đều là tam giác có ba cạnh bằng nhau. Do đó, công thức tính chu vi hình tam giác đều rất đơn giản:
Công thức:
P = 3a
Trong đó:
- P là chu vi hình tam giác (đơn vị đo: cm, m, km,...)
- a là độ dài một cạnh của hình tam giác đều (đơn vị đo: cm, m, km,...)
Ví dụ:
Một hình tam giác đều có độ dài mỗi cạnh là 5cm. Chu vi hình tam giác đều đó là:
P = 3a = 3 x 5cm = 15cm
Công thức tính chu vi hình tam giác cân
Hình tam giác cân là tam giác có hai cạnh bằng nhau. Do đó, công thức tính chu vi hình tam giác cân có dạng:
Công thức:
P = 2a + b
Trong đó:
- P là chu vi hình tam giác (đơn vị đo: cm, m, km,...)
- a là độ dài hai cạnh bằng nhau của hình tam giác (đơn vị đo: cm, m, km,...)
- b là độ dài cạnh còn lại của hình tam giác (đơn vị đo: cm, m, km,...)
Ví dụ:
Một hình tam giác cân có hai cạnh bằng nhau là 6cm và cạnh còn lại là 4cm. Chu vi hình tam giác cân đó là:
P = 2a + b = 2 x 6cm + 4cm = 16cm
Công thức tính chu vi hình tam giác lớp 3
Đối với học sinh lớp 3, công thức tính chu vi hình tam giác thường được đơn giản hóa thành:
Công thức:
C = a + b + c
Trong đó:
- C là chu vi hình tam giác (đơn vị đo: cm, m, km,...)
- a, b, c là độ dài ba cạnh của hình tam giác (đơn vị đo: cm, m, km,...)
Ví dụ:
Một hình tam giác có ba cạnh lần lượt là 5cm, 6cm và 7cm. Chu vi hình tam giác đó là:
C = 5cm + 6cm + 7cm = 18cm
Công thức tính chu vi hình tam giác lớp 5
Ở lớp 5, học sinh được học sâu hơn về các loại tam giác và các công thức tính chu vi của chúng. Ngoài công thức chung đã đề cập ở trên, các công thức sau cũng được học:
- Công thức tính chu vi hình tam giác vuông:
C = a + b + √(a² + b²)
- Công thức tính chu vi hình tam giác đều:
C = 3a
- Công thức tính chu vi hình tam giác cân:
C = 2a + b
Ví dụ:
Một hình tam giác vuông có hai cạnh góc vuông là 8cm và 10cm. Chu vi hình tam giác vuông đó là:
C = 8cm + 10cm + √(8² + 10²) = 8cm + 10cm + 12,8cm = 30,8cm
Công thức tính chu vi hình tam giác lớp 4
Ở lớp 4, học sinh bắt đầu học về hình học nên công thức tính chu vi hình tam giác được đơn giản hóa như sau:
Công thức:
P = a + b + c
Trong đó:
- P là chu vi hình tam giác (đơn vị đo: cm, m, km,...)
- a, b, c là độ dài ba cạnh của hình tam giác (đơn vị đo: cm, m, km,...)
Ví dụ:
Một hình tam giác có ba cạnh lần lượt là 4cm, 5cm và 6cm. Chu vi hình tam giác đó là:
P = 4cm + 5cm + 6cm = 15cm
Công thức tính chu vi hình tam giác lớp 2
Ở lớp 2, học sinh chưa được học về khái niệm chu vi nhưng có thể làm quen với phép tính cộng để tìm độ dài tổng các cạnh của hình tam giác.
Công thức:
Độ dài tổng các cạnh = a + b + c
Trong đó:
- a, b, c là độ dài ba cạnh của hình tam giác (đơn vị đo: cm, m, km,...)
Ví dụ:
Một hình tam giác có ba cạnh lần lượt là 2cm, 3cm và 4cm. Độ dài tổng các cạnh của hình tam giác đó là:
Độ dài tổng các cạnh = 2cm + 3cm + 4cm = 9cm
Công thức tính chu vi hình tam giác lớp 10
Ở lớp 10, học sinh được học sâu hơn về hình học phẳng và không gian, trong đó có các công thức tính chu vi của các loại đa giác, bao gồm cả hình tam giác.
Công thức:
- Công thức chung:
P = a + b + c
- Công thức tính chu vi hình tam giác vuông:
P = a + b + √(a² + b²)
- Công thức tính chu vi hình tam giác đều:
P = 3a
- Công thức tính chu vi hình tam giác cân:
P = 2a + b
Ví dụ:
Một hình tam giác cân có hai cạnh bằng nhau là 7cm và cạnh còn lại là 5cm. Chu vi hình tam giác cân đó là:
P = 2a + b = 2 x 7cm + 5cm = 19cm
Công thức tính chu vi hình đa giác
Ngoài hình tam giác, còn có nhiều loại đa giác khác, chẳng hạn như hình vuông, hình chữ nhật, hình bình hành, hình thoi. Dưới đây là các công thức tính chu vi của một số loại đa giác thường gặp:
- Hình vuông: P = 4a (trong đó a là độ dài một cạnh của hình vuông)
- Hình chữ nhật: P = 2(a + b) (trong đó a và b lần lượt là độ dài hai cạnh của hình chữ nhật)
- Hình bình hành: P = 2(a + b) (trong đó a và b lần lượt là độ dài hai cạnh kề nhau của hình bình hành)
- Hình thoi: P = 4a (trong đó a là độ dài một cạnh của hình thoi)
Kết luận
Công thức tính chu vi hình tam giác là một phần quan trọng trong kiến thức hình học. Hy vọng bài viết này đã cung cấp cho bạn đầy đủ các công thức và ví dụ để hiểu và áp dụng vào các bài toán thực tế. Hãy cố gắng luyện tập và nâng cao kỹ năng tính toán của mình để có thể giải quyết các bài toán liên quan đến hình tam giác một cách dễ dàng. Chúc bạn thành công!
Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!
Link nội dung: https://luathoanhut.vn/cong-thuc-tinh-chu-vi-hinh-tam-giac-a23722.html