
Đường trung tuyến là gì?
Đường trung tuyến là một trong những khái niệm cơ bản và quan trọng trong hình học tam giác. Đường trung tuyến giúp chúng ta hiểu sâu hơn về cấu trúc và tính chất của tam giác, hỗ trợ cho việc giải quyết nhiều bài toán hình học. Trong bài viết này, chúng ta sẽ tìm hiểu chi tiết về định nghĩa, cách gọi khác, tính chất và ứng dụng của đường trung tuyến trong hình học tam giác.
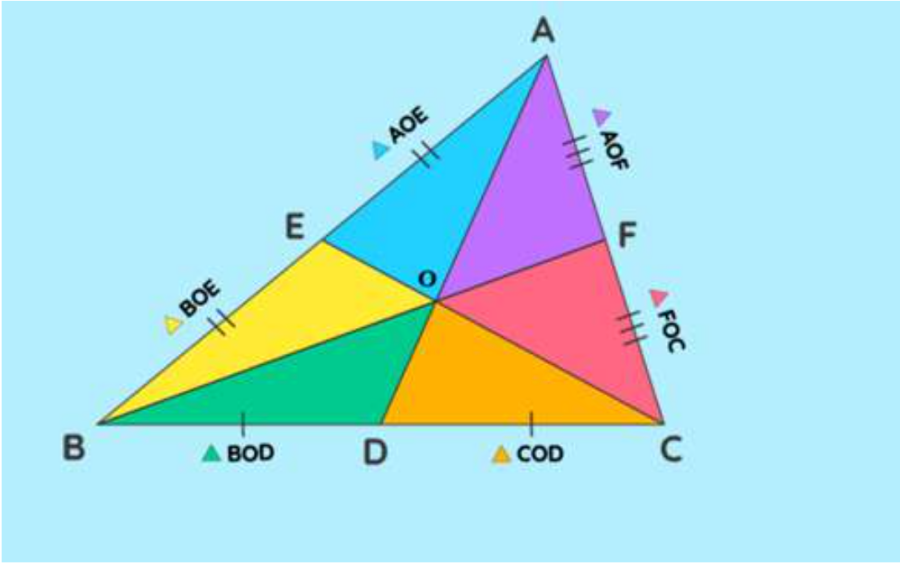
Định nghĩa: Đường trung tuyến của tam giác là đoạn thẳng nối một đỉnh của tam giác với điểm chính giữa của cạnh đối diện.
Nói cách khác, đường trung tuyến là đường thẳng chia đôi một cạnh của tam giác và đi qua đỉnh đối diện với cạnh đó. Trong một tam giác, có ba đường trung tuyến tương ứng với ba cạnh.
Đường trung tuyến gọi là gì?
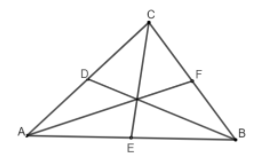
Ngoài tên gọi là "đường trung tuyến", khái niệm này còn được gọi bằng một số tên khác, bao gồm:
- Đường trung trực của đoạn thẳng
- Đường phân giác của góc đỉnh
Đường trung trực của đoạn thẳng: Do đường trung tuyến chia đôi một cạnh của tam giác, nên nó cũng là đường trung trực của đoạn thẳng đó.
Đường phân giác của góc đỉnh: Đường trung tuyến đi qua đỉnh và chia đôi một cạnh đối diện cũng đóng vai trò như đường phân giác của góc tạo bởi hai cạnh còn lại.
Đường trung tuyến là gì lớp 7?
Trong chương trình toán học lớp 7, đường trung tuyến được giới thiệu như một khái niệm quan trọng liên quan đến tam giác. Nội dung học tập liên quan đến đường trung tuyến ở lớp 7 bao gồm:
Phát hiện và vẽ đường trung tuyến của tam giác
Để phát hiện và vẽ đường trung tuyến của tam giác, ta thực hiện theo các bước sau:
- Xác định điểm chính giữa của một cạnh bất kỳ.
- Nối điểm này với đỉnh đối diện của cạnh đó.
- Đoạn thẳng tạo thành là đường trung tuyến của tam giác.
Tính chất của đường trung tuyến
Đường trung tuyến có một số tính chất quan trọng, bao gồm:
- Độ dài của đường trung tuyến bằng nửa cạnh đối diện.
- Đường trung tuyến chia tam giác thành hai tam giác có diện tích bằng nhau.
- Ba đường trung tuyến của một tam giác đồng quy tại một điểm (gọi là trọng tâm).
- Trọng tâm của một tam giác chia mỗi đường trung tuyến theo tỉ lệ 2:1.
Ứng dụng của đường trung tuyến trong giải bài toán
Đường trung tuyến là một công cụ hữu ích trong việc giải nhiều bài toán hình học liên quan đến tam giác. Một số ứng dụng phổ biến của đường trung tuyến bao gồm:
- Tính độ dài các cạnh và góc của tam giác
- Xác định trọng tâm của tam giác
- Chứng minh các tính chất của tam giác
Đường trung tuyến là gì tính chất?
Như đã đề cập ở trên, đường trung tuyến có một số tính chất quan trọng giúp chúng ta giải quyết các bài toán hình học liên quan đến tam giác.
Độ dài đường trung tuyến
Độ dài của đường trung tuyến ứng với cạnh $a$ trong tam giác $ABC$ được tính theo công thức:
m_a = $\fracm$.
Giao 3 đường trung tuyến là gì?
Giao điểm của ba đường trung tuyến của một tam giác được gọi là trọng tâm của tam giác.
Trọng tâm là điểm nằm ở bên trong tam giác
Trọng tâm của một tam giác nằm ở bên trong tam giác, không nằm trên bất kỳ cạnh nào của tam giác.
Trọng tâm chia mỗi đường trung tuyến theo tỉ lệ 2:1
Như đã đề cập ở trên, trọng tâm chia mỗi đường trung tuyến theo tỉ lệ 2:1.
Trọng tâm là điểm cân bằng của tam giác
Trọng tâm của một tam giác là điểm cân bằng của tam giác. Điều này có nghĩa là nếu treo tam giác trên trọng tâm, tam giác sẽ cân bằng và không bị nghiêng về bất kỳ phía nào.
Đường trung tuyến là đường phân giác
Đường trung tuyến ứng với một cạnh cũng là đường phân giác của góc tạo bởi hai cạnh còn lại của tam giác.
Đường trung tuyến là đường thẳng trung tuyến
Đường trung tuyến là đường thẳng nối đỉnh của tam giác với điểm chính giữa của cạnh đối diện.
Tính đường trung tuyến là gì?
Để tính độ dài đường trung tuyến của một tam giác, ta sử dụng công thức:
m_a = $\frac$aTrong đó:
- $m_a$ là độ dài đường trung tuyến ứng với cạnh $a$
- $a$ là độ dài cạnh đối diện với đường trung tuyến $m_a$
Đường trung tuyến của tam giác là gì?
Đường trung tuyến của tam giác là đoạn thẳng nối một đỉnh của tam giác với điểm chính giữa của cạnh đối diện.
Đường trung tuyến tiếng anh là gì?
Tiếng Anh của đường trung tuyến là "median".
Đường trung tuyến trong tam giác là gì?
Đường trung tuyến trong tam giác là đoạn thẳng nối một đỉnh của tam giác với điểm chính giữa của cạnh đối diện.
Đường trung trực trung tuyến là gì?
Đường trung trực trung tuyến là đường thẳng vuông góc với đường trung tuyến tại điểm chính giữa của cạnh đối diện.
Giao điểm 2 đường trung tuyến là gì?
Giao điểm của hai đường trung tuyến của một tam giác là điểm chia mỗi đường trung tuyến theo tỉ lệ 2:1.
Giao của 3 đường trung tuyến là gì?
Giao của ba đường trung tuyến của một tam giác là trọng tâm của tam giác.
Độ dài đường trung tuyến là gì?
Độ dài đường trung tuyến ứng với cạnh $a$ trong tam giác $ABC$ được tính theo công thức:
m_a = $\frac$a
Trong đó:
- $m_a$ là độ dài đường trung tuyến ứng với cạnh $a$
- $a$ là độ dài cạnh đối diện với đường trung tuyến $m_a$
Công thức đường trung tuyến là gì?
Công thức tính độ dài đường trung tuyến ứng với cạnh $a$ trong tam giác $ABC$ là:
m_a = $\frac$a
Trong đó:
- $m_a$ là độ dài đường trung tuyến ứng với cạnh $a$
- $a$ là độ dài cạnh đối diện với đường trung tuyến $m_a$
Kết luận
Đường trung tuyến là một khái niệm cơ bản và quan trọng trong hình học tam giác. Hiểu rõ định nghĩa, tính chất và ứng dụng của đường trung tuyến sẽ giúp chúng ta giải quyết nhiều bài toán hình học một cách hiệu quả và chính xác. Ngoài ra, đường trung tuyến còn có vai trò quan trọng trong việc xác định các điểm đặc biệt của tam giác như trọng tâm và giao điểm của ba đường trung tuyến. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về đường trung tuyến và các tính chất của nó.
Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!
Link nội dung: https://luathoanhut.vn/duong-trung-tuyen-la-gi-a23864.html