Góc đồng vị là gì? Cách chứng minh hai góc đồng vị?

Góc đồng vị là gì?

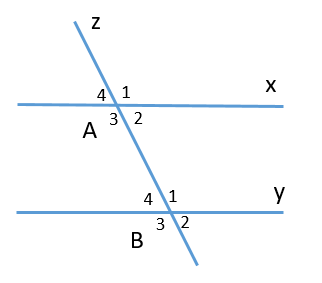
Định nghĩa góc đồng vị

Trước tiên, để hiểu rõ về góc đồng vị, chúng ta cần biết định nghĩa cơ bản của góc trong hình học. Góc là phần không gian được tạo thành bởi hai tia xuất phát từ một điểm chung, được đo bằng đơn vị độ. Khi hai góc có số đo bằng nhau, chúng được gọi là góc đồng vị.

Tính chất của góc đồng vị

Góc đồng vị có một số tính chất quan trọng:

1. Hai góc đồng vị bằng nhau.
2. Nếu hai góc là góc đồng vị, thì góc bù của chúng cũng đồng vị với nhau.
3. Góc đồng vị có thể được sử dụng để chứng minh tính chất của các hình học khác.

Cách chứng minh hai góc đồng vị bằng nhau

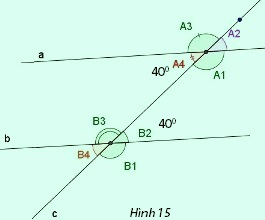
Phương pháp chứng minh trực tiếp

Để chứng minh hai góc đồng vị bằng nhau, chúng ta thường sử dụng phương pháp chứng minh trực tiếp. Cụ thể, ta cần chứng minh rằng hai góc có cùng số đo thông qua việc so sánh các yếu tố như tia, cạnh, hoặc các hình học khác.

Phương pháp chứng minh gián tiếp

Ngoài ra, chúng ta cũng có thể sử dụng phương pháp chứng minh gián tiếp để chứng minh hai góc đồng vị bằng nhau. Thay vì so sánh trực tiếp số đo của hai góc, chúng ta có thể chứng minh bằng cách sử dụng các tính chất hình học khác.

Ứng dụng của góc đồng vị trong hình học

Góc đồng vị có rất nhiều ứng dụng trong hình học, đặc biệt là trong việc chứng minh các bài toán liên quan đến góc và đường thẳng. Dưới đây là một số ví dụ về cách áp dụng góc đồng vị trong hình học:

1. Chứng minh tính chất của tam giác: Bằng cách sử dụng góc đồng vị, chúng ta có thể chứng minh các tính chất của tam giác như đối xứng, bằng cạnh, bằng góc.
2. Chứng minh tính chất của hình học phẳng: Góc đồng vị cũng được sử dụng để chứng minh tính chất của các hình học phẳng như hình vuông, hình chữ nhật, hay hình thang.
3. Chứng minh tính chất của đường thẳng: Góc đồng vị giúp chúng ta chứng minh tính chất của các đường thẳng như song song, trung tuyến, hay đường chéo.

Liên hệ giữa góc đồng vị và giao điểm của hai đường thẳng

Khi giải các bài toán hình học liên quan đến góc đồng vị, chúng ta thường phải xem xét đến liên hệ giữa góc đồng vị và giao điểm của hai đường thẳng. Cụ thể, khi hai đường thẳng cắt nhau, chúng ta có thể sử dụng góc đồng vị để chứng minh các tính chất của các góc tạo bởi các đường thẳng đó.

Ví dụ minh họa

Xét ví dụ sau: Cho hai đường thẳng AB và CD cắt nhau tại điểm O. Gọi E là giao điểm của AC và BD. Chứng minh rằng hai góc AOE và COB là góc đồng vị.

Giải pháp:

• Ta có AB // CD (do đề bài cho hai đường thẳng cắt nhau).
• Do đó, theo tính chất của góc đồng vị, ta có góc AOE = góc COB.

Từ ví dụ trên, chúng ta có thể thấy rằng việc áp dụng góc đồng vị giúp chúng ta chứng minh các tính chất của các góc tạo bởi các đường thẳng một cách dễ dàng và logic.

Mối quan hệ giữa góc đồng vị và tính song song của các đường thẳng

Một trong những ứng dụng quan trọng của góc đồng vị là trong việc chứng minh tính song song của các đường thẳng. Khi giải các bài toán liên quan đến tính song song của các đường thẳng, chúng ta thường sử dụng góc đồng vị để chứng minh tính chất này.

Phép chứng minh bằng góc đồng vị

Để chứng minh hai đường thẳng AB và CD song song, chúng ta thường sử dụng phép chứng minh bằng góc đồng vị. Cụ thể, nếu ta chứng minh được rằng hai góc tạo bởi hai đường thẳng và một đường chéo cắt chúng là góc đồng vị, thì ta có thể kết luận rằng hai đường thẳng đó là song song.

Ví dụ minh họa

Xét ví dụ sau: Cho hai đường thẳng AB và CD, với AC là đường chéo cắt chúng. Gọi E là giao điểm của AB và CD. Chứng minh rằng AB // CD.

Giải pháp:

• Ta có góc AEC = góc DEC (góc đồng vị).
• Do đó, theo tính chất của góc đồng vị, ta có AB // CD.

Từ ví dụ trên, chúng ta có thể thấy rằng việc sử dụng góc đồng vị giúp chúng ta chứng minh tính song song của các đường thẳng một cách hiệu quả và chính xác.

Định nghĩa góc đồng vị theo tiếng Anh

In geometry, two angles are said to be vertically opposite angles if the pairs of non-adjacent angles formed by two intersecting lines are equal. This property is known as the vertical angle theorem or the vertical angle property.

Ví dụ minh họa về góc đồng vị

Để hiểu rõ hơn về góc đồng vị, chúng ta cùng xem xét một ví dụ minh họa sau:

Ví dụ: Cho hai góc x và y. Biết rằng góc x + góc y = 180 độ. Chứng minh rằng hai góc đó là góc đồng vị.

Giải pháp:

• Ta có góc x + góc y = 180 độ.
• Do đó, hai góc x và y là góc đồng vị.

Từ ví dụ trên, chúng ta có thể thấy rằng việc chứng minh hai góc đồng vị bằng nhau có thể dựa vào các tính chất cơ bản của góc để giải quyết các bài toán hình học.

Bài tập liên quan đến góc đồng vị

Để nắm vững kiến thức về góc đồng vị, chúng ta cùng thực hành một số bài tập sau:

1. Chứng minh rằng hai góc đồng vị bằng nhau.
2. Chứng minh tính song song của hai đường thẳng bằng góc đồng vị.
3. Áp dụng góc đồng vị để chứng minh tính chất của các hình học khác.

Tài liệu tham khảo về góc đồng vị

Để tìm hiểu sâu hơn về góc đồng vị, bạn có thể tham khảo các tài liệu sau:

1. "Geometry Essentials For Dummies" by Mark Ryan.
2. "Introduction to Geometry" by Richard Rusczyk.
3. "Euclidean Geometry in Mathematical Olympiads" by Evan Chen.

Kết luận

Trong bài viết này, chúng ta đã tìm hiểu về khái niệm góc đồng vị là gì, cách chứng minh hai góc đồng vị bằng nhau, và ứng dụng của góc đồng vị trong hình học. Việc hiểu và áp dụng góc đồng vị không chỉ giúp chúng ta giải quyết các bài toán hình học một cách dễ dàng và logic, mà còn mở ra một cánh cửa mới trong việc khám phá và tìm hiểu về các tính chất hình học của các hình học phẳng. Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về góc đồng vị và cách áp dụng nó trong hình học.

Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!