Hướng dẫn tính khoảng cách từ một điểm đến một đường thẳng (chi tiết)

Hướng dẫn chi tiết về cách tính khoảng cách từ một điểm đến một đường thẳng

Phương pháp tính khoảng cách từ một điểm đến một đường thẳng

Để tính khoảng cách từ một điểm đến một đường thẳng, chúng ta có thể sử dụng một số phương pháp sau:

1. Sử dụng công thức Euclid: Đây là phương pháp đơn giản nhất để tính khoảng cách từ một điểm đến một đường thẳng. Công thức này dựa trên việc tính toán độ dài của đoạn thẳng nối điểm đó với đường thẳng.
2. Sử dụng vector: Một phương pháp khác là sử dụng khái niệm vector để tính khoảng cách. Bằng cách sử dụng tích vô hướng hoặc tích có hướng của vector, chúng ta có thể xác định khoảng cách một cách chính xác.

Các bước tính khoảng cách từ một điểm đến một đường thẳng

Để tính khoảng cách từ một điểm đến một đường thẳng, chúng ta có thể thực hiện các bước sau:

1. Xác định phương trình của đường thẳng.
2. Tìm vector chỉ phương của đường thẳng.
3. Tìm vector chỉ phương của đoạn thẳng nối điểm đến đường thẳng.
4. Sử dụng công thức Euclid hoặc phép chiếu vector để tính khoảng cách.

Ứng dụng của việc tính khoảng cách từ một điểm đến một đường thẳng

Việc tính khoảng cách từ một điểm đến một đường thẳng có rất nhiều ứng dụng trong thực tế, bao gồm:

• Trong định vị GPS: Xác định vị trí của một điểm so với một tuyến đường.
• Trong thiết kế đồ họa: Xác định khoảng cách từ một điểm đến một đường thẳng để tạo ra các hiệu ứng hình ảnh.
• Trong xây dựng: Đo lường khoảng cách từ một điểm đến một đường thẳng để xác định vị trí cắt của các đường dẫn.

Ví dụ minh họa về cách tính khoảng cách từ một điểm đến một đường thẳng

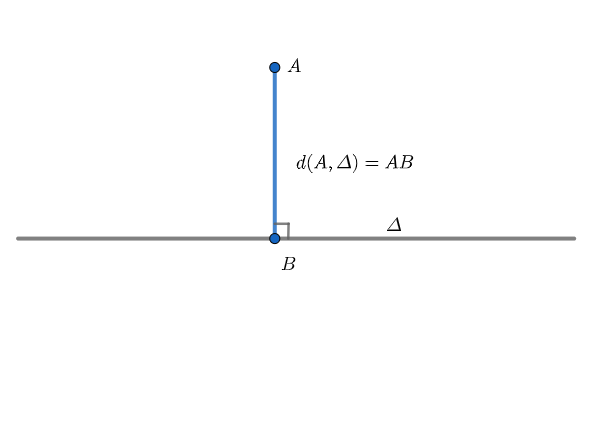
Bài toán ví dụ 1:

Giả sử có một đường thẳng có phương trình $y = 2x + 3$ và một điểm $A(1, 5)$. Hãy tính khoảng cách từ điểm $A$ đến đường thẳng đã cho.

Giải pháp:

1. Xác định vector chỉ phương của đường thẳng: $\vec$.

Những lưu ý khi tính khoảng cách từ một điểm đến một đường thẳng

Khi thực hiện tính toán khoảng cách từ một điểm đến một đường thẳng, cần lưu ý một số điểm sau:

• Xác định rõ phương trình của đường thẳng và tọa độ của điểm trước khi thực hiện tính toán.
• Sử dụng các công thức và phương pháp tính toán phù hợp với bài toán cụ thể.
• Kiểm tra kết quả sau khi tính toán để đảm bảo tính chính xác của quá trình.

Các công cụ hỗ trợ tính khoảng cách từ một điểm đến một đường thẳng

Để thuận tiện trong việc tính toán khoảng cách từ một điểm đến một đường thẳng, có thể sử dụng các công cụ hỗ trợ như:

• Công cụ tính toán trực tuyến: Có nhiều trang web cung cấp công cụ tính khoảng cách từ một điểm đến một đường thẳng mà bạn có thể sử dụng miễn phí.
• Phần mềm đồ họa: Các phần mềm như AutoCAD, Mathematica cũng cung cấp tính năng tính khoảng cách giúp bạn thực hiện các bài toán liên quan đến đường thẳng và điểm.

Tầm quan trọng của việc tính khoảng cách từ một điểm đến một đường thẳng

Việc tính khoảng cách từ một điểm đến một đường thẳng không chỉ giúp chúng ta hiểu rõ về vị trí tương đối giữa các đối tượng mà còn có ứng dụng rộng rãi trong thực tế. Từ việc xác định vị trí trong không gian đến việc thiết kế các sản phẩm công nghệ, tính toán khoảng cách từ một điểm đến một đường thẳng đóng vai trò quan trọng trong quá trình nghiên cứu và ứng dụng.

Kết luận

Tính khoảng cách từ một điểm đến một đường thẳng là một phần quan trọng của toán học và có nhiều ứng dụng thực tế. Qua bài viết này, chúng ta đã tìm hiểu chi tiết về cách tính khoảng cách này, các phương pháp, bước thực hiện, ví dụ minh họa và ứng dụng của việc tính khoảng cách từ một điểm đến một đường thẳng. Hy vọng rằng những kiến thức này sẽ giúp bạn hiểu rõ hơn về chủ đề này và áp dụng vào thực tế một cách linh hoạt.

Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!