Tổng hợp Công thức tính diện tích, chu vi, thể tích hình các cơ bản

Công thức tính diện tích, chu vi tam giác đều

Định nghĩa và đặc điểm của tam giác đều

Tam giác đều là một hình tam giác có ba cạnh bằng nhau và ba góc bằng nhau, mỗi góc bằng 60 độ. Đây là một trong những hình học cơ bản và quan trọng, thường được sử dụng trong nhiều ứng dụng thực tế như kiến trúc, thiết kế, nghiên cứu khoa học, v.v.

Công thức tính diện tích tam giác đều

Diện tích của tam giác đều có thể được tính bằng công thức sau:

Diện tích = (√3/4) × a^2

Trong đó, a là chiều dài của mỗi cạnh tam giác.

Công thức tính chu vi tam giác đều

Chu vi của tam giác đều được tính bằng cách nhân 3 lần chiều dài của một cạnh:

Chu vi = 3 × a

Trong đó, a là chiều dài của mỗi cạnh tam giác.

Ứng dụng của tam giác đều

Tam giác đều có nhiều ứng dụng thú vị, chẳng hạn như:

1. Trong thiết kế kiến trúc, tam giác đều được sử dụng để tạo nên các kết cấu vững chắc và đẹp mắt.
2. Trong nghiên cứu khoa học, tam giác đều được sử dụng để mô hình hóa các cấu trúc tinh thể và phân tử.
3. Trong nghệ thuật và thiết kế, tam giác đều được sử dụng để tạo ra các mẫu hình học đẹp mắt và hài hòa.

Công thức tính diện tích, chu vi hình chữ nhật

Định nghĩa và đặc điểm của hình chữ nhật

Hình chữ nhật là một hình phẳng có bốn cạnh, trong đó hai cạnh đối diện bằng nhau và hai góc đối diện bằng nhau. Đây là một hình học cơ bản và được sử dụng rộng rãi trong nhiều lĩnh vực.

Công thức tính diện tích hình chữ nhật

Diện tích của hình chữ nhật được tính bằng công thức:

Diện tích = chiều dài × chiều rộng

Trong đó, chiều dài và chiều rộng là hai kích thước của hình chữ nhật.

Công thức tính chu vi hình chữ nhật

Chu vi của hình chữ nhật được tính bằng công thức:

Chu vi = 2 × (chiều dài + chiều rộng)

Trong đó, chiều dài và chiều rộng là hai kích thước của hình chữ nhật.

Ứng dụng của hình chữ nhật

Hình chữ nhật có nhiều ứng dụng trong cuộc sống, chẳng hạn như:

1. Trong thiết kế kiến trúc, hình chữ nhật được sử dụng rộng rãi để tạo nên các công trình.
2. Trong thiết kế đồ nội thất và bao bì sản phẩm, hình chữ nhật được sử dụng để tạo ra các sản phẩm thẩm mỹ và hiệu quả.
3. Trong nghiên cứu khoa học, hình chữ nhật được sử dụng để mô hình hóa và phân tích các hệ thống.

Công thức tính diện tích, chu vi hình thang

Định nghĩa và đặc điểm của hình thang

Hình thang là một hình phẳng có bốn cạnh, trong đó hai cạnh đối diện song song và hai cạnh còn lại không song song. Đây là một hình học cơ bản và được sử dụng trong nhiều ứng dụng thực tế.

Công thức tính diện tích hình thang

Diện tích của hình thang được tính bằng công thức:

Diện tích = (1/2) × (đáy trên + đáy dưới) × chiều cao

Trong đó, đáy trên và đáy dưới là hai cạnh song song, và chiều cao là khoảng cách giữa hai cạnh song song.

Công thức tính chu vi hình thang

Chu vi của hình thang được tính bằng công thức:

Chu vi = a + b + c + d

Trong đó, a, b, c và d là chiều dài của bốn cạnh hình thang.

Ứng dụng của hình thang

Hình thang có nhiều ứng dụng trong cuộc sống, chẳng hạn như:

1. Trong thiết kế kiến trúc, hình thang được sử dụng để tạo nên các mái vòm và các cấu trúc nghiêng.
2. Trong nghiên cứu khoa học, hình thang được sử dụng để mô hình hóa và phân tích các hệ thống tự nhiên.
3. Trong nghệ thuật và thiết kế, hình thang được sử dụng để tạo ra các mẫu hình học độc đáo và sáng tạo.

Công thức tính diện tích, chu vi hình bình hành

Định nghĩa và đặc điểm của hình bình hành

Hình bình hành là một hình phẳng có bốn cạnh, trong đó hai cạnh đối diện bằng nhau và song song, và hai góc đối diện bằng nhau. Đây là một hình học cơ bản và được sử dụng rộng rãi trong nhiều lĩnh vực.

Công thức tính diện tích hình bình hành

Diện tích của hình bình hành được tính bằng công thức:

Diện tích = cơ số × chiều cao

Trong đó, cơ số là chiều dài của một cạnh bất kỳ, và chiều cao là khoảng cách giữa hai cạnh song song.

Công thức tính chu vi hình bình hành

Chu vi của hình bình hành được tính bằng công thức:

Chu vi = 2 × (cơ số + chiều cao)

Trong đó, cơ số và chiều cao là hai thông số cơ bản của hình bình hành.

Ứng dụng của hình bình hành

Hình bình hành có nhiều ứng dụng trong cuộc sống, chẳng hạn như:

1. Trong thiết kế kiến trúc, hình bình hành được sử dụng để tạo nên các cấu trúc nghiêng và độc đáo.
2. Trong nghiên cứu khoa học, hình bình hành được sử dụng để mô hình hóa và phân tích các hệ thống tự nhiên.
3. Trong nghệ thuật và thiết kế, hình bình hành được sử dụng để tạo ra các mẫu hình học sáng tạo và độc đáo.

Công thức tính diện tích, chu vi hình thoi

Định nghĩa và đặc điểm của hình thoi

Hình thoi là một hình phẳng có bốn cạnh, trong đó hai cặp cạnh đối diện bằng nhau và song song. Đây là một hình học cơ bản và được sử dụng rộng rãi trong nhiều lĩnh vực.

Công thức tính diện tích hình thoi

Diện tích của hình thoi được tính bằng công thức:

Diện tích = (1/2) × d1 × d2

Trong đó, d1 và d2 là hai đường chéo của hình thoi.

Công thức tính chu vi hình thoi

Chu vi của hình thoi được tính bằng công thức:

Chu vi = 4 × a

Trong đó, a là chiều dài của một cạnh bất kỳ của hình thoi.

Ứng dụng của hình thoi

Hình thoi có nhiều ứng dụng trong cuộc sống, chẳng hạn như:

1. Trong thiết kế kiến trúc, hình thoi được sử dụng để tạo nên các cấu trúc độc đáo và sáng tạo.
2. Trong nghiên cứu khoa học, hình thoi được sử dụng để mô hình hóa và phân tích các hệ thống tự nhiên.
3. Trong nghệ thuật và thiết kế, hình thoi được sử dụng để tạo ra các mẫu hình học tinh tế và hài hòa.

Công thức tính diện tích, chu vi hình tròn

Định nghĩa và đặc điểm của hình tròn

Hình tròn là một hình phẳng có tất cả các điểm trên đường cong cách tâm một khoảng bằng nhau. Đây là một hình học cơ bản và được sử dụng rộng rãi trong nhiều lĩnh vực.

Công thức tính diện tích hình tròn

Diện tích của hình tròn được tính bằng công thức:

Diện tích = π × r^2

Trong đó, r là bán kính của hình tròn.

Công thức tính chu vi hình tròn

Chu vi của hình tròn được tính bằng công thức:

Chu vi = 2 × π × r

Trong đó, r là bán kính của hình tròn.

Ứng dụng của hình tròn

Hình tròn có nhiều ứng dụng trong cuộc sống, chẳng hạn như:

1. Trong thiết kế kiến trúc, hình tròn được sử dụng để tạo nên các cấu trúc như tháp, vòm và lốp xe.
2. Trong nghiên cứu khoa học, hình tròn được sử dụng để mô hình hóa và phân tích các hệ thống tự nhiên như các hành tinh, sao, v.v.
3. Trong nghệ thuật và thiết kế, hình tròn được sử dụng để tạo ra các mẫu hình học đẹp mắt và hài hòa.

Công thức tính diện tích, thể tích hình lập phương

Định nghĩa và đặc điểm của hình lập phương

Hình lập phương là một hình học cơ bản trong không gian, có sáu mặt bằng nhau và mỗi cạnh bằng nhau. Đây là một hình học quan trọng và được sử dụng rộng rãi trong nhiều lĩnh vực.

Công thức tính diện tích mặt lập phương

Diện tích của mỗi mặt lập phương được tính bằng công thức:

Diện tích mặt = a^2

Trong đó, a là chiều dài cạnh lập phương.

Công thức tính thể tích hình lập phương

Thể tích của hình lập phương được tính bằng công thức:

Thể tích = a^3

Trong đó, a là chiều dài cạnh lập phương.

Ứng dụng của hình lập phương

Hình lập phương có nhiều ứng dụng trong cuộc sống, chẳng hạn như:

1. Trong thiết kế kiến trúc, hình lập phương được sử dụng để tạo nên các cấu trúc như nhà, tòa nhà, v.v.
2. Trong nghiên cứu khoa học, hình lập phương được sử dụng để mô hình hóa và phân tích các cấu trúc tinh thể và phân tử.
3. Trong công nghệ, hình lập phương được sử dụng để thiết kế và sản xuất các sản phẩm như hộp, thùng chứa, v.v.

Công thức tính diện tích, thể tích hình hộp chữ nhật

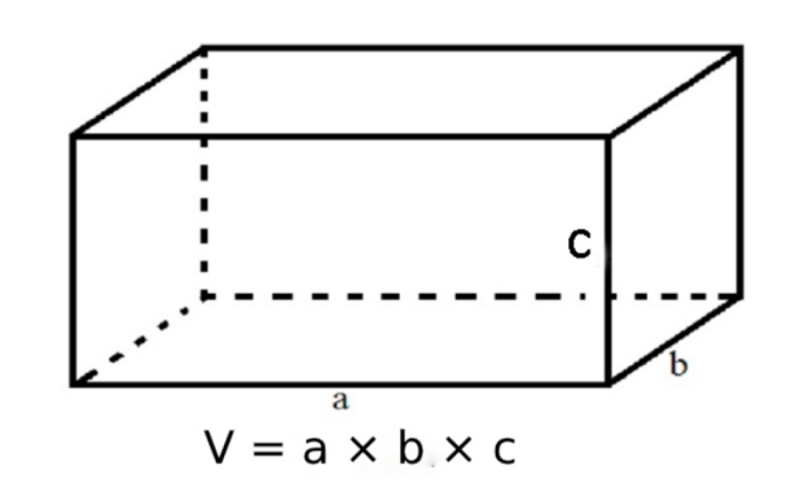
Định nghĩa và đặc điểm của hình hộp chữ nhật

Hình hộp chữ nhật là một hình học cơ bản trong không gian, có sáu mặt chữ nhật và mỗi cạnh có chiều dài khác nhau. Đây là một hình học quan trọng và được sử dụng rộng rãi trong nhiều lĩnh vực.

Công thức tính diện tích mặt hộp chữ nhật

Diện tích của mỗi mặt hộp chữ nhật được tính bằng công thức:

Diện tích mặt = dài × rộng

Trong đó, dài và rộng là chiều dài và chiều rộng của mỗi mặt.

Công thức tính thể tích hình hộp chữ nhậtThể tích của hình hộp chữ nhật được tính bằng công thức:

Thể tích = dài × rộng × cao

Trong đó, dài, rộng và cao lần lượt là chiều dài, chiều rộng và chiều cao của hình hộp chữ nhật.

Ứng dụng của hình hộp chữ nhật

Hình hộp chữ nhật có nhiều ứng dụng trong cuộc sống, chẳng hạn như:

1. Trong thiết kế kiến trúc, hình hộp chữ nhật được sử dụng để tạo nên các cấu trúc như nhà, tòa nhà, v.v.
2. Trong ngành công nghiệp, hình hộp chữ nhật được sử dụng để đóng gói và vận chuyển hàng hóa.
3. Trong nghệ thuật và thiết kế, hình hộp chữ nhật được sử dụng để tạo ra các sản phẩm đa dạng từ giấy, carton đến gỗ và kim loại.

Công thức tính diện tích, thể tích hình cầu

Định nghĩa và đặc điểm của hình cầu

Hình cầu là một hình học không gian có tất cả các điểm trên bề mặt cách một điểm gọi là tâm một khoảng bằng nhau. Đây là một hình học quan trọng và được áp dụng rộng rãi trong nhiều lĩnh vực.

Công thức tính diện tích bề mặt hình cầu

Diện tích bề mặt của hình cầu được tính bằng công thức:

Diện tích bề mặt = 4 × π × r^2

Trong đó, r là bán kính của hình cầu.

Công thức tính thể tích hình cầu

Thể tích của hình cầu được tính bằng công thức:

Thể tích = (4/3) × π × r^3

Trong đó, r là bán kính của hình cầu.

Ứng dụng của hình cầu

Hình cầu có nhiều ứng dụng trong cuộc sống, chẳng hạn như:

1. Trong ngành công nghiệp, hình cầu được sử dụng để thiết kế các bình chứa, bóng đèn, v.v.
2. Trong y học, hình cầu được sử dụng để mô hình hóa các cơ quan và tế bào trong cơ thể con người.
3. Trong công nghệ, hình cầu được sử dụng để thiết kế các ống dẫn, bi, vòng bi, v.v.

Kết luận

Trên đây là các công thức tính diện tích, chu vi, thể tích của một số hình học cơ bản như tam giác, hình chữ nhật, hình thang, hình bình hành, hình thoi, hình tròn, hình lập phương, hình hộp chữ nhật và hình cầu. Việc hiểu và áp dụng các công thức này không chỉ giúp chúng ta giải quyết các bài toán mà còn giúp chúng ta hiểu rõ hơn về các hình học và ứng dụng của chúng trong cuộc sống hàng ngày.

Hy vọng rằng thông qua bài viết này, bạn đã có cái nhìn tổng quan về các công thức cơ bản và ứng dụng của hình học trong thực tế. Hãy áp dụng kiến thức này vào thực hành để phát triển tư duy logic và khả năng giải quyết vấn đề của mình. Chúc các bạn thành công!

Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!