Tính chất của hai tiếp tuyến cắt nhau

Đặc tính của hai tiếp tuyến cắt nhau

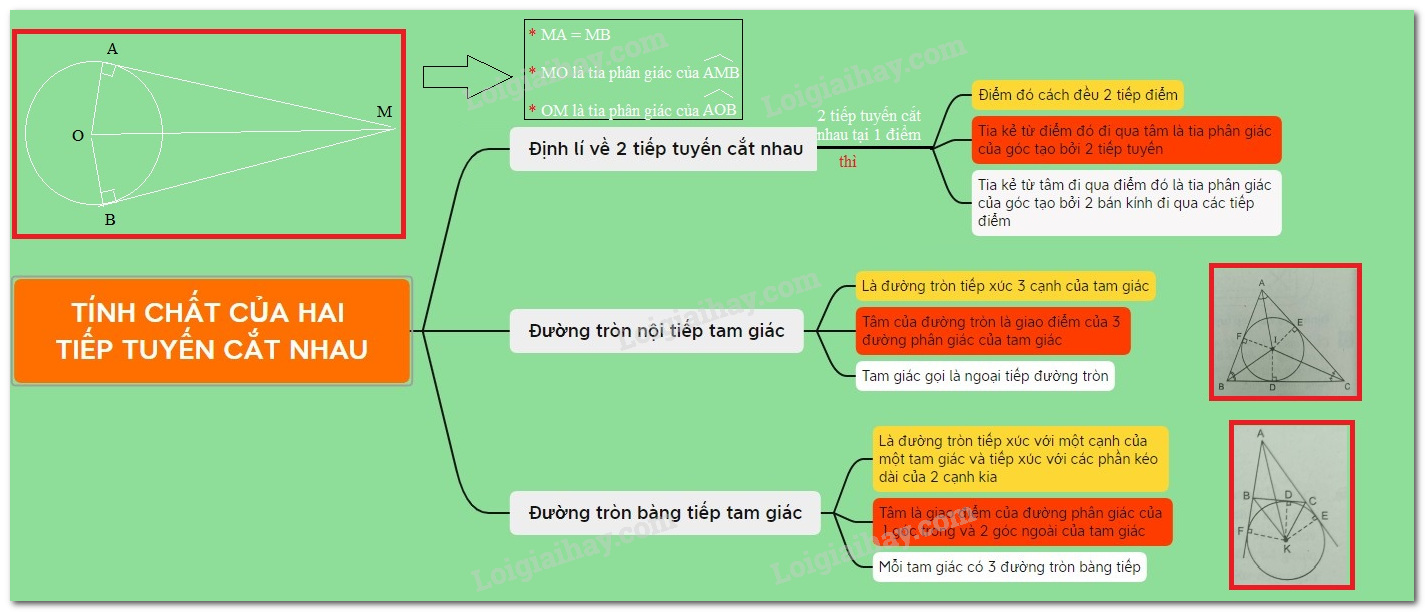
Khi hai tiếp tuyến cắt nhau, chúng ta sẽ thu được một số đặc tính nổi bật.

Tính chất song song của tiếp tuyến tại giao điểm

Tại giao điểm của hai tiếp tuyến, chúng luôn song song với nhau. Điều này có nghĩa là, nếu chúng ta kéo dài hai tiếp tuyến ra, chúng sẽ không bao giờ gặp nhau. Hai tiếp tuyến này tạo với nhau một góc bằng 0 độ.

Để chứng minh tính chất này, chúng ta có thể sử dụng định lý về tiếp tuyến của đường tròn. Theo định lý này, tiếp tuyến luôn vuông góc với đường kính đi qua điểm tiếp xúc. Vì vậy, tại giao điểm của hai tiếp tuyến, chúng sẽ luôn song song với nhau.

Độ dài của đoạn thẳng nối tâm đường tròn với giao điểm

Một đặc điểm khác của hai tiếp tuyến cắt nhau là độ dài của đoạn thẳng nối tâm đường tròn với giao điểm. Độ dài này luôn bằng nhau, không phụ thuộc vào vị trí của hai tiếp tuyến.

Để chứng minh, chúng ta có thể sử dụng tính chất của tam giác vuông. Tại giao điểm của hai tiếp tuyến, chúng ta có thể hình dung được một tam giác vuông, trong đó một cạnh là đoạn thẳng nối tâm đường tròn với giao điểm. Theo tính chất của tam giác vuông, hai đoạn thẳng này luôn bằng nhau.

Tính chất góc tạo bởi tiếp tuyến và dây cung

Khi hai tiếp tuyến cắt nhau, chúng tạo với nhau một góc nhất định. Góc này luôn bằng góc tạo bởi tiếp tuyến và dây cung tương ứng. Điều này có thể được chứng minh bằng cách sử dụng định lý về góc nội tiếp.

Theo định lý này, góc nội tiếp bằng một nửa góc tạo bởi hai tiếp tuyến. Vì vậy, góc tạo bởi hai tiếp tuyến sẽ bằng hai lần góc nội tiếp, tức là bằng góc tạo bởi tiếp tuyến và dây cung.

Tính chất góc tạo bởi hai tiếp tuyến

Ngoài ra, góc tạo bởi hai tiếp tuyến cũng có một số đặc điểm riêng. Cụ thể, góc này luôn bằng 90 độ, hay nói cách khác, hai tiếp tuyến cắt nhau theo một góc vuông.

Để chứng minh tính chất này, chúng ta có thể sử dụng định lý về tiếp tuyến của đường tròn. Theo định lý này, tiếp tuyến luôn vuông góc với đường kính đi qua điểm tiếp xúc. Vì vậy, tại giao điểm của hai tiếp tuyến, chúng sẽ tạo với nhau một góc vuông.

Tính chất góc tạo bởi tiếp tuyến và bán kính

Một đặc điểm khác của hai tiếp tuyến cắt nhau là góc tạo bởi tiếp tuyến và bán kính. Góc này luôn bằng 45 độ.

Để chứng minh điều này, chúng ta có thể sử dụng định lý về tam giác đều. Tại giao điểm của hai tiếp tuyến, chúng ta có thể hình dung được một tam giác đều, trong đó một cạnh là đoạn thẳng nối tâm đường tròn với giao điểm. Theo tính chất của tam giác đều, các góc của tam giác này sẽ bằng 60 độ. Vì vậy, góc giữa tiếp tuyến và bán kính sẽ bằng 45 độ.

Tính chất song song của tiếp tuyến tại giao điểm

Như đã đề cập ở trên, khi hai tiếp tuyến cắt nhau, chúng luôn song song với nhau tại giao điểm. Điều này có nghĩa là, nếu chúng ta kéo dài hai tiếp tuyến ra, chúng sẽ không bao giờ gặp nhau.

Chứng minh tính chất song song bằng định lý về tiếp tuyến

Để chứng minh tính chất này, chúng ta có thể sử dụng định lý về tiếp tuyến của đường tròn. Theo định lý này, tiếp tuyến luôn vuông góc với đường kính đi qua điểm tiếp xúc.

Xét hai tiếp tuyến cắt nhau tại điểm M. Tại điểm M, chúng ta có thể kẻ một đường kính đi qua điểm M. Theo định lý về tiếp tuyến, hai tiếp tuyến sẽ vuông góc với đường kính này. Vì vậy, hai tiếp tuyến sẽ song song với nhau.

Ý nghĩa của tính chất song song

Tính chất song parallel của hai tiếp tuyến tại giao điểm có ý nghĩa rất quan trọng trong hình học. Nó giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các yếu tố trong một đường tròn.

Đồng thời, tính chất này cũng rất hữu ích trong việc giải quyết các bài toán liên quan đến tiếp tuyến. Khi biết rằng hai tiếp tuyến luôn song song, chúng ta có thể dễ dàng tìm ra các thông tin cần thiết để giải bài toán.

Độ dài của đoạn thẳng nối tâm đường tròn với giao điểm

Một đặc điểm khác của hai tiếp tuyến cắt nhau là độ dài của đoạn thẳng nối tâm đường tròn với giao điểm. Độ dài này luôn bằng nhau, không phụ thuộc vào vị trí của hai tiếp tuyến.

Chứng minh bằng tính chất của tam giác vuông

Để chứng minh tính chất này, chúng ta có thể sử dụng tính chất của tam giác vuông. Tại giao điểm của hai tiếp tuyến, chúng ta có thể hình dung được một tam giác vuông, trong đó một cạnh là đoạn thẳng nối tâm đường tròn với giao điểm.

Theo tính chất của tam giác vuông, hai đoạn thẳng này luôn bằng nhau. Điều này có nghĩa là, bất kể vị trí của hai tiếp tuyến như thế nào, độ dài của đoạn thẳng nối tâm đường tròn với giao điểm sẽ luôn bằng nhau.

Ý nghĩa của tính chất độ dài bằng nhau

Tính chất này có ý nghĩa quan trọng trong việc giải quyết các bài toán liên quan đến tiếp tuyến. Khi biết rằng độ dài của đoạn thẳng nối tâm đường tròn với giao điểm luôn bằng nhau, chúng ta có thể dễ dàng tìm ra các thông tin cần thiết để giải bài toán.

Ngoài ra, tính chất này cũng giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các yếu tố trong một đường tròn. Từ đó, chúng ta có thể vận dụng kiến thức này vào việc giải quyết các bài toán hình học khác.

Tính chất góc tạo bởi tiếp tuyến và dây cung

Khi hai tiếp tuyến cắt nhau, chúng tạo với nhau một góc nhất định. Góc này luôn bằng góc tạo bởi tiếp tuyến và dây cung tương ứng.

Chứng minh bằng định lý về góc nội tiếp

Để chứng minh tính chất này, chúng ta có thể sử dụng định lý về góc nội tiếp. Theo định lý này, góc nội tiếp bằng một nửa góc tạo bởi hai tiếp tuyến.

Xét hai tiếp tuyến cắt nhau tại điểm M. Tại điểm M, chúng ta có thể kẻ một dây cung tương ứng. Theo định lý về góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung sẽ bằng một nửa góc tạo bởi hai tiếp tuyến.

Vì vậy, góc tạo bởi hai tiếp tuyến sẽ bằng hai lần góc tạo bởi tiếp tuyến và dây cung.

Ý nghĩa của tính chất góc

Tính chất này có ý nghĩa quan trọng trong việc giải quyết các bài toán liên quan đến tiếp tuyến. Khi biết rằng góc tạo bởi hai tiếp tuyến bằng hai lần góc tạo bởi tiếp tuyến và dây cung, chúng ta có thể dễ dàng tìm ra các thông tin cần thiết để giải bài toán.

Ngoài ra, tính chất này cũng giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các yếu tố trong một đường tròn. Từ đó, chúng ta có thể vận dụng kiến thức này vào việc giải quyết các bài toán hình học khác.

Tính chất góc tạo bởi hai tiếp tuyến

Ngoài ra, góc tạo bởi hai tiếp tuyến cũng có một số đặc điểm riêng. Cụ thể, góc này luôn bằng 90 độ, hay nói cách khác, hai tiếp tuyến cắt nhau theo một góc vuông.

Chứng minh bằng định lý về tiếp tuyến

Để chứng minh tính chất này, chúng ta có thể sử dụng định lý về tiếp tuyến của đường tròn. Theo định lý này, tiếp tuyến luôn vuông góc với đường kính đi qua điểm tiếp xúc.

Xét hai tiếp tuyến cắt nhau tại điểm M. Tại điểm M, chúng ta có thể kẻ một đường kính đi qua điểm M. Theo định lý về tiếp tuyến, hai tiếp tuyến sẽ vuông góc với đường kính này. Vì vậy, hai tiếp tuyến sẽ tạo với nhau một góc vuông, tức là 90 độ.

Ý nghĩa của tính chất góc vuông

Tính chất này có ý nghĩa rất quan trọng trong hình học. Nó giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các yếu tố trong một đường tròn.

Đồng thời, tính chất này cũng rất hữu ích trong việc giải quyết các bài toán liên quan đến tiếp tuyến. Khi biết rằng hai tiếp tuyến tạo với nhau một góc vuông, chúng ta có thể dễ dàng tìm ra các thông tin cần thiết để giải bài toán.

Tính chất góc tạo bởi tiếp tuyến và bán kính

Một đặc điểm khác của hai tiếp tuyến cắt nhau là góc tạo bởi tiếp tuyến và bán kính. Góc này luôn bằng 45 độ.

Chứng minh bằng tính chất của tam giác đều

Để chứng minh điều này, chúng ta có thể sử dụng định lý về tam giác đều. Tại giao điểm của hai tiếp tuyến, chúng ta có thể hình dung được một tam giác đều, trong đó một cạnh là đoạn thẳng nối tâm đường tròn với giao điểm.

Theo tính chất của tam giác đều, các góc của tam giác này sẽ bằng nhau và mỗi góc sẽ bằng 60 độ. Do đó, góc tạo bởi tiếp tuyến và bán kính sẽ bằng một nửa của góc trong tam giác đều, tức là 30 độ. Vì vậy, góc tạo bởi tiếp tuyến và bán kính sẽ luôn bằng 45 độ.

Ý nghĩa của tính chất góc 45 độ

Tính chất này cũng rất quan trọng trong việc giải quyết các bài toán hình học liên quan đến đường tròn. Khi biết rằng góc tạo bởi tiếp tuyến và bán kính luôn bằng 45 độ, chúng ta có thể áp dụng kiến thức này để giải quyết các bài toán phức tạp hơn.

Ngoài ra, tính chất này cũng giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các yếu tố trong một đường tròn. Từ đó, chúng ta có thể áp dụng kiến thức này vào việc giải quyết các bài toán hình học khác.

Công thức liên hệ giữa độ dài hai tiếp tuyến và đoạn thẳng nối hai tiếp điểm

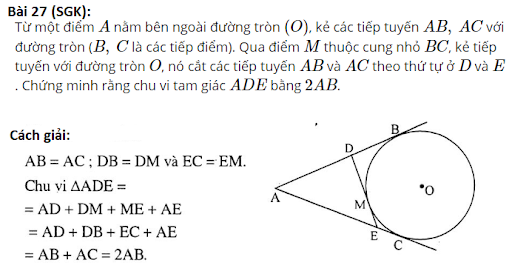
Một công thức quan trọng trong hình học đường tròn là công thức liên hệ giữa độ dài hai tiếp tuyến và đoạn thẳng nối hai tiếp điểm. Công thức này giúp chúng ta tính toán độ dài của hai tiếp tuyến mà không cần phải vẽ hình.

Công thức tính độ dài hai tiếp tuyến

Giả sử hai tiếp tuyến AB và AC cắt nhau tại điểm A trên đường tròn. Để tính độ dài của hai tiếp tuyến này, chúng ta có thể sử dụng công thức sau:

[AB^2 = AC \times AD]

Trong đó, AB là độ dài của một tiếp tuyến, AC là độ dài từ điểm A đến tâm đường tròn, và AD là độ dài từ điểm A đến điểm tiếp xúc trên đường tròn.

Ý nghĩa của công thức

Công thức này giúp chúng ta tính toán độ dài của hai tiếp tuyến một cách nhanh chóng và chính xác. Khi áp dụng công thức này, chúng ta có thể dễ dàng giải quyết các bài toán liên quan đến tiếp tuyến mà không cần phải vẽ hình.

Ngoài ra, công thức này cũng giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các yếu tố trong một đường tròn. Từ đó, chúng ta có thể áp dụng kiến thức này vào việc giải quyết các bài toán hình học khác.

Ứng dụng tính chất hai tiếp tuyến cắt nhau trong giải toán

Tính chất của hai tiếp tuyến cắt nhau có rất nhiều ứng dụng trong việc giải các bài toán hình học liên quan đến đường tròn. Dưới đây là một số ví dụ minh họa về cách áp dụng tính chất này vào việc giải các bài toán.

Ví dụ 1

Cho một đường tròn (O) và hai tiếp tuyến AB và CD cắt nhau tại điểm M. Biết rằng AM = 6 cm, MB = 4 cm, và MC = 3 cm. Hỏi độ dài của MD là bao nhiêu?

Giải

Ta có công thức liên hệ giữa độ dài hai tiếp tuyến và đoạn thẳng nối hai tiếp điểm:

[AB^2 = AC \times AD]

Áp dụng vào trường hợp này, ta có:

[6^2 = 4 \times (4 + x)]

Suy ra x = 5 cm.

Vậy độ dài của MD là 5 cm.

Ví dụ 2

Cho một đường tròn (O) và hai tiếp tuyến PQ và RS cắt nhau tại điểm T. Biết rằng PT = 8 cm, QT = 6 cm, và RT = 5 cm. Hỏi độ dài của ST là bao nhiêu?

Giải

Tương tự như ví dụ trước, ta có:

[PQ^2 = PR \times PS]

Áp dụng vào trường hợp này, ta có:

[8^2 = 6 \times (5 + x)]

Suy ra x = 7 cm.

Vậy độ dài của ST là 7 cm.

Bài tập tính chất hai tiếp tuyến cắt nhau

1. Cho đường tròn (O) và hai tiếp tuyến AB, CD cắt nhau tại điểm M. Biết rằng AM = 5 cm, MB = 3 cm, và MC = 4 cm. Tính độ dài của MD.
2. Cho đường tròn (O) và hai tiếp tuyến PQ, RS cắt nhau tại điểm T. Biết rằng PT = 7 cm, QT = 4 cm, và RT = 6 cm. Tính độ dài của ST.

Hãy thử giải các bài tập trên để rèn luyện kỹ năng và hiểu biết về tính chất của hai tiếp tuyến cắt nhau.

Kết luận

Trên đây là những tính chất cơ bản và quan trọng của hai tiếp tuyến cắt nhau trên đường tròn. Việc hiểu và áp dụng những tính chất này sẽ giúp chúng ta giải quyết các bài toán hình học liên quan đến đường tròn một cách dễ dàng và chính xác. Hy vọng rằng thông qua bài viết này, bạn đã có cái nhìn tổng quan về tính chất của hai tiếp tuyến cắt nhau và cách áp dụng chúng vào việc giải các bài toán. Chúc bạn thành công trong việc học tập và rèn luyện kỹ năng giải bài toán hình học!

Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!