Thể tích hình hộp chữ nhật: Công thức tính và ứng dụng

1. Công thức tính thể tích hình hộp chữ nhật

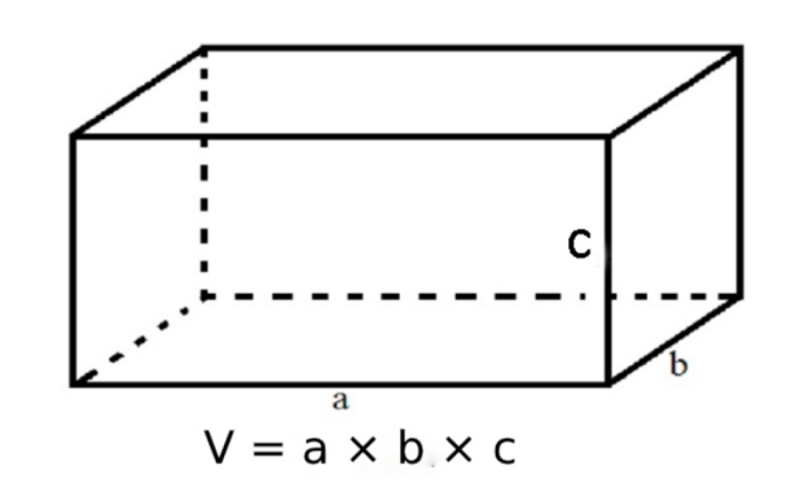
Công thức tính thể tích hình hộp chữ nhật là:

V = abc

trong đó:

• V là thể tích của hình hộp chữ nhật (đơn vị khối)
• a là chiều dài của hình hộp chữ nhật (đơn vị chiều dài)
• b là chiều rộng của hình hộp chữ nhật (đơn vị chiều dài)
• c là chiều cao của hình hộp chữ nhật (đơn vị chiều dài)

1.1. Đơn vị thể tích

Đơn vị thể tích phổ biến nhất đối với hình hộp chữ nhật là mét khối (m³). Các đơn vị thể tích khác cũng có thể được sử dụng, chẳng hạn như:

• Xăng ti mét khối (cm³): 1 cm³ = 10^-6 m³
• Lít (l): 1 l = 10^-3 m³
• Quả galông (gal): 1 gal ≈ 0,003785 m³

1.2. Biến đổi công thức

Công thức thể tích hình hộp chữ nhật có thể được biến đổi để tìm chiều dài, chiều rộng hoặc chiều cao của hình bằng cách chia công thức cho các đại lượng tương ứng:

• a = V/bc
• b = V/ac
• c = V/ab

2. Công thức tính thể tích khối vuông

Khối vuông là một trường hợp đặc biệt của hình hộp chữ nhật có ba chiều dài bằng nhau, thường được gọi là cạnh của khối. Do đó, công thức thể tích khối vuông được rút gọn thành:

V = a³

trong đó a là cạnh của khối vuông (đơn vị chiều dài).

2.1. Đơn vị thể tích khối vuông

Đơn vị thể tích khối vuông thường là mét khối (m³), xăng ti mét khối (cm³), inch khối (in³) hoặc cm khối (cm³).

2.2. Biến đổi công thức

Công thức thể tích khối vuông có thể được biến đổi để tìm độ dài cạnh của khối bằng cách sử dụng căn bậc ba của thể tích:

a = V^(1/3)

3. Áp dụng công thức tính thể tích hình hộp chữ nhật

3.1. Tính thể tích hộp quà

Một hộp quà có chiều dài, chiều rộng và chiều cao lần lượt là 25 cm, 15 cm và 10 cm. Thể tích của hộp quà là:

V = abc = 25 cm x 15 cm x 10 cm = 3750 cm³

3.2. Xác định chiều dài của bể bơi

Một bể bơi có chiều rộng 5m, chiều cao 2m và thể tích 100m³. Chiều dài của bể bơi là:

a = V/bc = 100m³ / (5m x 2m) = 10m

4. Tính thể tích hình hộp chữ nhật có dạng khối

4.1. Khối gỗ hình hộp chữ nhật

Một khối gỗ hình hộp chữ nhật có thể tích 120 cm³, chiều dài gấp đôi chiều rộng và gấp ba lần chiều cao. Tìm kích thước của khối gỗ.

Giả sử chiều rộng của khối gỗ là x cm. Khi đó:

• Chiều dài: 2x cm
• Chiều cao: x/3 cm

Thế vào công thức thể tích, ta được:

120 cm³ = (2x cm)(x cm)(x/3 cm)

=> x = 6 cm

Kích thước của khối gỗ là:

• Chiều rộng: 6 cm
• Chiều dài: 12 cm
• Chiều cao: 2 cm

4.2. Khối bê tông hình hộp vuông

Một khối bê tông hình hộp vuông có thể tích 27m³. Tìm độ dài cạnh của khối bê tông.

Gọi cạnh của khối bê tông là a (m). Khi đó:

27 m³ = a³

=> a = 3 m

Độ dài cạnh của khối bê tông là 3m.

5. So sánh thể tích hình hộp chữ nhật

5.1. Thể tích so sánh hai hoặc nhiều hình hộp chữ nhật

Cho hai hoặc nhiều hình hộp chữ nhật với kích thước khác nhau, ta có thể so sánh thể tích của chúng bằng cách nhân các kích thước của từng hình lại với nhau. Hình nào có tích lớn hơn thì có thể tích lớn hơn.

5.2. So sánh thể tích dựa trên tỷ lệ

Nếu các hình hộp chữ nhật có tỷ lệ chiều dài, chiều rộng và chiều cao giống nhau, thì ta có thể so sánh thể tích của chúng dựa trên tỷ lệ kích thước. Ví dụ:

• Nếu hình hộp chữ nhật A có chiều dài gấp đôi hình hộp chữ nhật B, thì thể tích của A cũng gấp đôi thể tích của B.
• Nếu hình hộp chữ nhật A có chiều rộng gấp ba hình hộp chữ nhật B, thì thể tích của A cũng gấp ba thể tích của B.

6. Ứng dụng của thể tích hình hộp chữ nhật

6.1. Xây dựng và kiến trúc

• Xác định thể tích đất đào trong quá trình đào móng nhà.
• Tính toán thể tích bể bơi, bể nước, bể chứa.
• Ước tính lượng vật liệu xây dựng cần thiết như bê tông, gạch, đá.

6.2. Giao thông và vận tải

• Xác định thể tích hàng hóa trong xe tải, tàu hỏa hoặc máy bay.
• Xác định thể tích nhiên liệu trong bình xăng, dầu của các phương tiện giao thông.
• Ước tính không gian lưu trữ cần thiết trong kho bãi và trung tâm hậu cần.

6.3. Nông nghiệp và nuôi trồng thủy sản

• Xác định thể tích đất trong vườn trồng trọt.
• Tính toán thể tích nước trong ao nuôi cá, hồ chứa.
• Ước tính sản lượng nông nghiệp theo thể tích.

6.4. Công nghiệp

• Xác định thể tích sản phẩm trong các thùng chứa, hộp bảo quản.
• Tính toán thể tích nguyên liệu cần thiết cho quá trình sản xuất.
• Ước tính thể tích chất thải công nghiệp để xử lý và tái chế.

Kết luận

Thể tích hình hộp chữ nhật là một khái niệm quan trọng được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Công thức tính thể tích đơn giản và dễ áp dụng giúp chúng ta ước tính không gian và lượng vật chất một cách chính xác. Việc hiểu và áp dụng các công thức này đóng vai trò quan trọng trong quá trình thiết kế, xây dựng, vận tải, nông nghiệp và sản xuất công nghiệp, góp phần vào sự phát triển kinh tế và xã hội.

Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!