Công thức tính diện tích hình bình hành
Diện tích hình bình hành có thể được tính bằng nhiều công thức khác nhau, tùy thuộc vào các thông số đã biết. Dưới đây là một số công thức phổ biến nhất:
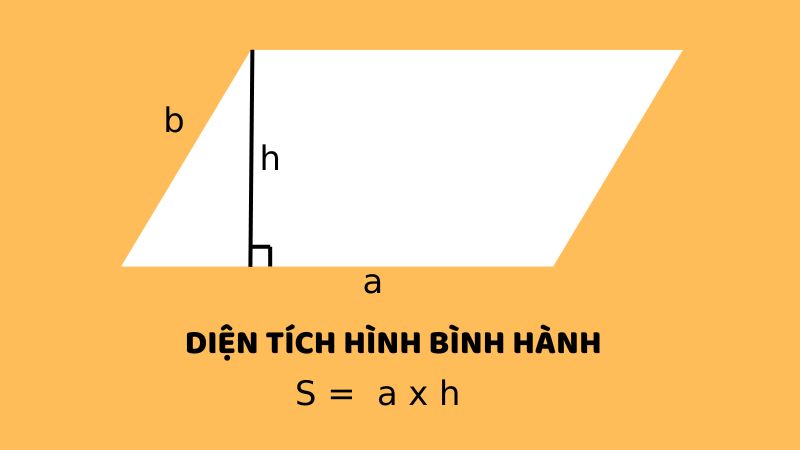
Công thức 1: Diện tích bằng độ dài một cạnh nhân với chiều cao tương ứng
Công thức này sử dụng chiều dài của một cạnh hình bình hành và chiều cao của hình bình hành (chiều cao là khoảng cách vuông góc từ cạnh đó đến cạnh đối diện song song).
- Công thức: S = a x h
- Trong đó:
- S là diện tích hình bình hành (đơn vị: m²)
- a là độ dài một cạnh hình bình hành (đơn vị: m)
- h là chiều cao tương ứng với cạnh a (đơn vị: m)
Ví dụ: Nếu một hình bình hành có cạnh AB = 10m và chiều cao CH = 8m, thì diện tích hình bình hành là:
S = a x h = 10m x 8m = 80m²
Công thức 2: Diện tích bằng tích hai cạnh kề nhân với sin góc giữa hai cạnh đó
Công thức này sử dụng độ dài của hai cạnh kề của hình bình hành và sin góc giữa hai cạnh đó.
- Công thức: S = a x b x sin C
- Trong đó:
- S là diện tích hình bình hành (đơn vị: m²)
- a và b là độ dài hai cạnh kề của hình bình hành (đơn vị: m)
- C là góc giữa cạnh a và cạnh b (đơn vị: độ)
Ví dụ: Nếu một hình bình hành có cạnh AB = 10m, cạnh BC = 6m và góc C = 60°, thì diện tích hình bình hành là:
S = a x b x sin C = 10m x 6m x sin 60° = 25,98m²
Công thức 3: Diện tích bằng một nửa tích độ dài hai đường chéo
Công thức này sử dụng độ dài của hai đường chéo của hình bình hành.
- Công thức: S = 1/2 x d1 x d2
- Trong đó:
- S là diện tích hình bình hành (đơn vị: m²)
- d1 và d2 là độ dài hai đường chéo của hình bình hành (đơn vị: m)
Ví dụ: Nếu một hình bình hành có đường chéo AC = 12m và đường chéo BD = 10m, thì diện tích hình bình hành là:
S = 1/2 x d1 x d2 = 1/2 x 12m x 10m = 60m²
Các dạng đặc biệt của hình bình hành
Ngoài công thức chung, diện tích hình bình hành còn có công thức riêng cho một số dạng đặc biệt:
Hình chữ nhật
Hình chữ nhật là một hình bình hành có bốn góc vuông. Đối với hình chữ nhật, diện tích còn có thể tính bằng cách nhân chiều dài với chiều rộng:
- Công thức: S = l x w
- Trong đó:
- S là diện tích hình chữ nhật (đơn vị: m²)
- l là chiều dài hình chữ nhật (đơn vị: m)
- w là chiều rộng hình chữ nhật (đơn vị: m)
Hình thoi
Hình thoi là một hình bình hành có bốn cạnh bằng nhau. Đối với hình thoi, diện tích còn có thể tính bằng cách nhân một nửa tích độ dài hai đường chéo:
- Công thức: S = 1/2 x d1 x d2
- Trong đó:
- S là diện tích hình thoi (đơn vị: m²)
- d1 và d2 là độ dài hai đường chéo của hình thoi (đơn vị: m)
Diện tích hình bình hành trong tọa độ
Trong hệ trục tọa độ, diện tích hình bình hành có thể được tính bằng cách sử dụng tọa độ các đỉnh của hình bình hành.
- Công thức: S = 1/2 x |(x1y2 - x2y1) + (x2y3 - x3y2) + (x3y4 - x4y3) + (x4y1 - x1y4)|
- Trong đó:
- (x1, y1), (x2, y2), (x3, y3), (x4, y4) là tọa độ các đỉnh của hình bình hành theo thứ tự
Ví dụ: Nếu một hình bình hành có tọa độ các đỉnh là A(1, 2), B(3, 4), C(5, 2) và D(3, 0), thì diện tích hình bình hành là:
S = 1/2 x |(1x4 - 3x2) + (3x2 - 5x2) + (5x2 - 3x2) + (3x0 - 1x2)| = 6
Các ứng dụng của tính diện tích hình bình hành
Tính diện tích hình bình hành có nhiều ứng dụng trong thực tế, bao gồm:
- Tính diện tích đất đai và bất động sản
- Tính diện tích mặt cắt ngang của các cấu trúc
- Tính diện tích bề mặt của các vật thể
- Tính thể tích của các khối lăng trụ
Bảng tóm tắt công thức tính diện tích hình bình hành
| Công thức | Ứng dụng | ||
|---|---|---|---|
| S = a x h | Tính diện tích bằng chiều dài một cạnh và chiều cao | ||
| S = a x b x sin C | Tính diện tích bằng tích hai cạnh kề và sin góc giữa hai cạnh đó | ||
| S = 1/2 x d1 x d2 | Tính diện tích bằng một nửa tích độ dài hai đường chéo | ||
| S = l x w | Tính diện tích hình chữ nhật (hình bình hành có bốn góc vuông) | ||
| S = 1/2 x d1 x d2 | Tính diện tích hình thoi (hình bình hành có bốn cạnh bằng nhau) | ||
| S = 1/2 x | (x1y2 - x2y1) + (x2y3 - x3y2) + (x3y4 - x4y3) + (x4y1 - x1y4) | Tính diện tích hình bình hành trong tọa độ |
Kết luận
Diện tích hình bình hành là một khái niệm hình học quan trọng có nhiều ứng dụng trong thực tế. Việc nắm vững các công thức tính diện tích hình bình hành là công cụ thiết yếu cho các chuyên gia trong các lĩnh vực như toán học, kiến trúc và xây dựng. Bằng cách hiểu rõ công thức và ứng dụng của chúng, chúng ta có thể giải quyết hiệu quả các bài toán liên quan đến diện tích hình bình hành và sử dụng kiến thức này để giải quyết các vấn đề khác nhau trong cuộc sống.
Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!

















