Bài viết này sẽ cung cấp một cái nhìn sâu sắc về diện tích mặt cầu, bao gồm các công thức, định lý liên quan và các ứng dụng thực tế của nó.
Định nghĩa và công thức diện tích mặt cầu
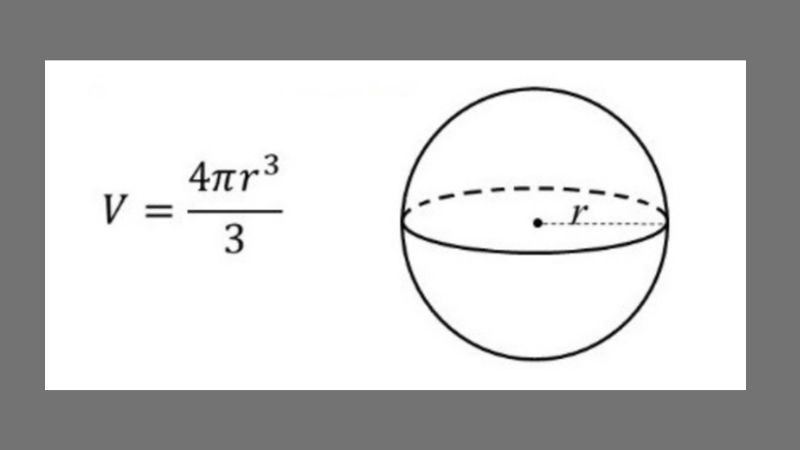
Định nghĩa: Diện tích mặt cầu là diện tích của bề mặt hình cầu.
Công thức: Diện tích mặt cầu có bán kính r được tính bằng công thức:
A = 4πr^2
trong đó:
- A là diện tích mặt cầu
- r là bán kính mặt cầu
Định lý liên quan đến diện tích mặt cầu
Ngoài công thức cơ bản, còn có một số định lý quan trọng liên quan đến diện tích mặt cầu:
Định lý tích vô hướng
Phát biểu: Diện tích mặt cầu bằng tích vô hướng của vectơ pháp tuyến đơn vị tại bất kỳ điểm nào trên bề mặt với vectơ dịch chuyển từ tâm đến điểm đó.
Định lý chụp hình cầu
Phát biểu: Diện tích mặt cầu bằng tổng diện tích của tất cả các đường tròn tạo thành mặt cầu khi cắt mặt cầu bằng một mặt phẳng bất kỳ.
Định lý mở rộng
Phát biểu: Diện tích mặt cầu nằm bên trong một khối nón có đỉnh tại tâm mặt cầu bằng diện tích hình tròn đáy khối nón nhân với hệ số thể tích mặt cầu (4/3π).
Ứng dụng của diện tích mặt cầu

Diện tích mặt cầu có nhiều ứng dụng thiết thực trong các lĩnh vực sau:
Vật lý và kỹ thuật
- Tính toán lưu lượng chất lỏng và khí trong các đường ống hình cầu
- Thiết kế vòm, mái vòm và các cấu trúc cong khác
- Xác định diện tích bề mặt của các vật thể hình cầu, như quả bóng, quả địa cầu và vệ tinh
Sinh học và y học
- Tính toán diện tích bề mặt của các tế bào và cơ quan hình cầu
- Thiết kế các hệ thống cung cấp thuốc và vắc-xin hình cầu
- Đo lường khối lượng cơ thể của trẻ em và người lớn
Địa lý và thiên văn học
- Xác định chu vi và diện tích bề mặt của Trái Đất, Mặt Trăng và các hành tinh khác
- Tính toán diện tích bề mặt của các thiên hà và cụm sao
Toán học và thống kê
- Mô hình hóa các phân phối xác suất hình cầu
- Xác định các phép đo hình ảnh, như hình elip
- Phân tích dữ liệu không gian và thống kê
Bảng tóm tắt công thức diện tích mặt cầu
| Trường hợp | Công thức |
|---|---|
| Mặt cầu bán kính r | A = 4πr^2 |
| Mặt cầu bên trong khối nón bán kính đáy r và chiều cao h | A = πr^2(4/3π) = 4/3πr^2h |
| Mặt cầu tạo bởi phép quay hình elip có trục chính a và trục phụ b | A = π(a^2 + b^2) |
Ví dụ về ứng dụng diện tích mặt cầu
Ví dụ 1: Tính diện tích bề mặt của một quả bóng rổ
Một quả bóng rổ có bán kính khoảng 12 cm. Diện tích bề mặt của quả bóng rổ là:
A = 4π(12 cm)^2 ≈ 565 cm^2
Ví dụ 2: Xác định diện tích bề mặt của một tế bào hình cầu
Một tế bào hình cầu có đường kính khoảng 10 μm. Diện tích bề mặt của tế bào là:
A = 4π(5 μm)^2 ≈ 314 μm^2
Ví dụ 3: Ước tính diện tích bề mặt của Trái Đất
Bán kính Trái Đất khoảng 6371 km. Diện tích bề mặt của Trái Đất là:
A = 4π(6371 km)^2 ≈ 510 triệu km^2
Kết luận
Diện tích mặt cầu là một khái niệm quan trọng trong nhiều lĩnh vực, cung cấp một biện pháp về lượng bề mặt của một hình cầu. Các công thức, định lý và ứng dụng khác nhau liên quan đến diện tích mặt cầu làm cho khái niệm này trở thành một công cụ mạnh mẽ để giải quyết các vấn đề trong vật lý, kỹ thuật, sinh học, địa lý và thậm chí cả toán học. Hiểu biết rõ về diện tích mặt cầu rất cần thiết cho các nhà khoa học, kỹ sư và bất kỳ ai làm việc với các vật thể hoặc hiện tượng hình cầu.
Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!

















