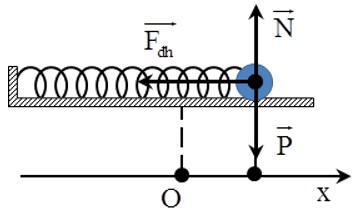
Các thành phần chính của con lắc lò xo
Vật nặng: Là một vật có khối lượng m, có thể là một quả cầu, một thanh kim loại hoặc bất kỳ vật nào khác có khối lượng.
Lò xo: Là một vật đàn hồi có độ cứng k, có thể là lò xo xoắn, lò xo lá hoặc bất kỳ loại lò xo nào khác có khả năng đàn hồi.
Lực đàn hồi: Là lực mà lò xo tác dụng lên vật nặng khi bị kéo giãn hoặc nén. Lực đàn hồi có phương trùng với phương của lò xo và có chiều ngược lại với chiều biến dạng của lò xo.
Định nghĩa tần số góc (ω) trong con lắc lò xo
Tần số góc (ω) của một con lắc lò xo là đại lượng đặc trưng cho tốc độ dao động của vật, được tính bằng:
ω = √(k/m)
Trong đó:
- k là độ cứng của lò xo (N/m)
- m là khối lượng của vật nặng (kg)
Ý nghĩa vật lý: Tần số góc là số dao động toàn phần mà vật thực hiện được trong 2π giây.
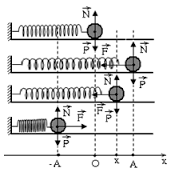
Phân tích hình ảnh GIF về con lắc lò xo
Hình ảnh GIF mô tả dao động của một con lắc lò xo gồm:
- Biên độ (A): Là li độ cực đại mà vật đạt được trong quá trình dao động.
- Chu kỳ (T): Là thời gian thực hiện một dao động toàn phần.
- Tần số (f): Là số dao động toàn phần thực hiện trong một giây.
Khái niệm con lắc lò xo
Con lắc lò xo là một hệ thống dao động cơ học gồm một vật nặng khối lượng $m$ được treo vào một lò xo có độ cứng $k$. Khi vật được kéo lệch khỏi vị trí cân bằng của nó và được thả ra, nó sẽ dao động quanh vị trí cân bằng do lực đàn hồi của lò xo tác dụng lên vật.
Vật nặng
Vật nặng là một vật có khối lượng $m$, có thể là một quả cầu, một thanh kim loại hoặc bất kỳ vật nào khác có khối lượng.
Lò xo
Lò xo là một vật đàn hồi có độ cứng $k$, có thể là lò xo xoắn, lò xo lá hoặc bất kỳ loại lò xo nào khác có khả năng đàn hồi.
Lực đàn hồi
Lực đàn hồi là lực mà lò xo tác dụng lên vật nặng khi bị kéo giãn hoặc nén. Lực đàn hồi có phương trùng với phương của lò xo và có chiều ngược lại với chiều biến dạng của lò xo.
Định luật bảo toàn năng lượng
Trong dao động của con lắc lò xo, cơ năng của hệ thống được chuyển hóa giữa động năng và thế năng đàn hồi. Tổng cơ năng của hệ thống luôn được bảo toàn, nghĩa là:
$$E = \fracmv^2$$
Trong đó:
- $E$ là tổng cơ năng của hệ thống
- $k$ là độ cứng của lò xo
- $A$ là biên độ dao động
- $m$ là khối lượng của vật nặng
- $v$ là vận tốc của vật nặng
Ứng dụng của con lắc lò xo
Con lắc lò xo có nhiều ứng dụng trong thực tế, chẳng hạn như:
- Làm bộ phận giảm xóc trong xe ô tô, xe máy và các thiết bị khác.
- Làm bộ phận cảm biến trong các thiết bị đo lường, chẳng như máy đo động đất, máy đo gia tốc.
- Làm bộ phận dao động trong các đồng hồ cơ học. Đặc biệt, con lắc lò xo có thể được sử dụng để cân bằng các đồng hồ trong điều kiện dao động và rung động.
- Làm bộ phận dao động trong các thiết bị giảm tiếng ồn.
Tính toán tần số góc (ω) trong con lắc lò xo
Tần số góc (ω) của một con lắc lò xo được tính bằng công thức:
ω = √(k/m)
Trong đó:
- $k$ là độ cứng của lò xo
- $m$ là khối lượng của vật nặng
Để tính được tần số góc của con lắc lò xo, ta cần xác định đơn vị đo của các đại lượng trước khi thay vào công thức.
Đơn vị đo của k và m
Đơn vị đo của độ cứng k: Độ cứng của lò xo được đo bằng đơn vị Newton/mét (N/m).
Đơn vị đo của khối lượng m: Khối lượng của vật được đo bằng đơn vị kilogram (kg).
Bài tập ví dụ: tính tần số góc ω của con lắc lò xo
Cho một con lắc lò xo có độ cứng $k=5N/m$ và khối lượng $m=2kg$. Hãy tính tần số góc $ω$ của con lắc lò xo.
Theo công thức, ta có:
ω = √(k/m)
= √(5/2)
≈ 3.16 (rad/s)
Với tần số góc sai số là 3.16 rad/s.
Đánh giá chất lượng dao động của con lắc lò xo
Để đánh giá chất lượng dao động của con lắc lò xo, người ta sử dụng đại lượng hệ số suy biến $Q$, được tính bằng công thức:
Q = ωT
Trong đó:
- $ω$ là tần số góc của con lắc lò xo
- $T$ là chu kỳ của dao động (tính bằng giây)
Hệ số suy biến càng lớn thì dao động của con lắc lò xo càng ít bị suy biến và trong thực tế, giá trị $Q$ thường chỉ tăng lên khi khối lượng vật nặng giảm hoặc độ cứng của lò xo tăng.
Phương trình con lắc lò xo

Phương trình con lắc lò xo dùng để mô tả quá trình dao động của con lắc lò xo theo thời gian. Phương trình này có dạng:
x(t) = Acos(ωt + φ)
Trong đó:
- $x(t)$ là biên độ của dao động tại thời điểm $t$
- $A$ là biên độ của dao động
- $ω$ là tần số góc của con lắc lò xo
- $t$ là thời gian
- $φ$ là pha ban đầu của dao động
Đánh giá chất lượng dao động bằng phương trình con lắc lò xo
Sử dụng phương trình con lắc lò xo, ta có thể dễ dàng tính toán và đánh giá chất lượng dao động của con lắc lò xo thông qua các đại lượng:
- Biên độ dao động (A): Thay giá trị $t=0$ vào phương trình để tính được biên độ $A$.
- Chu kỳ dao động (T): Tính theo công thức $T = \frac$.
- Vận tốc (v): Tính bằng đạo hàm của biên độ $x(t)$ theo thời gian $t$.
- Gia tốc (a): Tính bằng đạo hàm lần 2 của biên độ $x(t)$ theo thời gian $t$.
Kết luận
Như vậy, con lắc lò xo là một hệ thống dao động cơ học quan trọng và có nhiều ứng dụng trong thực tế. Tính toán tần số góc của con lắc lò xo giúp ta hiểu rõ hơn về quá trình dao động của nó và đánh giá được chất lượng dao động thông qua hệ số suy biến Q. Phương trình con lắc lò xo cũng giúp ta tính toán và đánh giá các đại lượng khác nhau liên quan đến dao động của con lắc lò xo. Hy vọng bài viết này sẽ giúp bạn hiểu thêm về khái niệm con lắc lò xo và các tính toán liên quan.
Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!

















