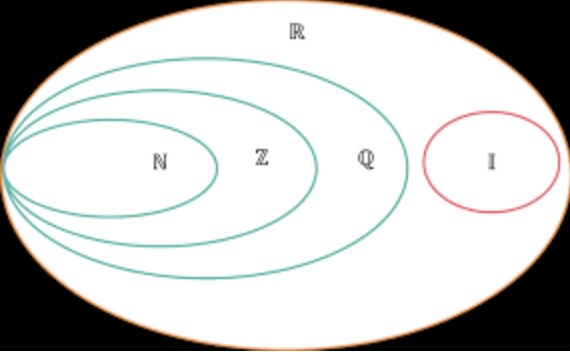
R là tập hợp số thực

Trong tập hợp số thực, có nhiều loại số khác nhau như số nguyên, số thập phân, số hữu tỉ, số vô tỉ, số dương, số âm và số không. Tập hợp số thực R bao gồm tất cả các số hữu tỉ và số vô tỉ. Để hiểu rõ hơn về tập hợp này, chúng ta cùng đi vào từng loại số trong R.
Tập hợp số hữu tỉ
Tập hợp số hữu tỉ bao gồm tất cả các số có thể biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên và b không bằng không. Ví dụ, 2/3, 5/4, 7/2 đều là các số hữu tỉ. Tập hợp số hữu tỉ cũng bao gồm tất cả các số nguyên, vì mỗi số nguyên đều có thể biểu diễn dưới dạng phân số với mẫu số bằng 1.
Tập hợp số vô tỉ
Tập hợp số vô tỉ bao gồm tất cả các số không thể biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên và b không bằng không. Ví dụ, √2, π, e đều là các số vô tỉ. Đây là những số không thể được viết dưới dạng phân số đơn giản nào.
Các tính chất của tập hợp số thực R
Tập hợp số thực có nhiều tính chất quan trọng, giúp chúng ta hiểu rõ hơn về tập hợp này và áp dụng vào các bài toán.
Tập hợp số thực là một tập hợp trù mật
Tập hợp số thực là một tập hợp trù mật, nghĩa là giữa hai số thực bất kỳ luôn có một số thực khác nằm giữa. Ví dụ, giữa hai số 1 và 2 luôn có một số thực nằm giữa, ví dụ như 1.5. Điều này cho thấy rằng tập hợp số thực không có khoảng cách lớn giữa các số, mỗi số đều có thể tiếp cận với nhau.
Tập hợp số thực là một tập hợp hoàn toàn có thứ tự
Tập hợp số thực là một tập hợp hoàn toàn có thứ tự, nghĩa là mọi số thực đều có thể so sánh với nhau bằng cách sử dụng các phép toán cộng, trừ, nhân và chia. Ví dụ, ta có thể so sánh số 3 và số 4 bằng cách thực hiện phép tính 3 + 1 và 4 + 1, từ đó suy ra được rằng 3 < 4. Điều này cho thấy rằng trong tập hợp số thực, ta có thể xác định được mối quan hệ giữa các số.
Tập hợp số thực là một tập hợp liên thông
Tập hợp số thực là một tập hợp liên thông, nghĩa là có thể đi từ bất kỳ số thực nào đến bất kỳ số thực nào khác mà không cần phải rời khỏi tập hợp số thực. Ví dụ, ta có thể đi từ số 1 đến số 2 bằng cách thực hiện các phép tính 1 + 1 và 2 - 1. Điều này cho thấy rằng trong tập hợp số thực, ta có thể di chuyển giữa các số một cách liên tục.
Ứng dụng của tập hợp số thực R
Tập hợp số thực được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau, từ toán học đến vật lý và kỹ thuật. Dưới đây là một số ứng dụng của tập hợp số thực R.
Toán học
Trong toán học, tập hợp số thực R được sử dụng để định nghĩa các khái niệm cơ bản như đường thẳng, đường cong, hình học, tích phân và vi phân. Ngoài ra, tập hợp số thực cũng được sử dụng để giải quyết các bài toán liên quan đến xác suất và thống kê.
Vật lý
Trong vật lý, tập hợp số thực R được sử dụng để mô tả các đại lượng vật lý như thời gian, không gian và khối lượng. Nó cũng được sử dụng để giải quyết các bài toán liên quan đến chuyển động và tương tác giữa các vật.
Kỹ thuật
Trong kỹ thuật, tập hợp số thực R được sử dụng để mô tả các đại lượng kỹ thuật như áp suất, nhiệt độ và điện áp. Nó cũng được sử dụng để giải quyết các bài toán liên quan đến thiết kế và xây dựng các công trình kỹ thuật.
R là tập hợp số gồm những gì?
R là tập hợp số thực, bao gồm tất cả các số hữu tỉ và số vô tỉ. Trong tập hợp này, có rất nhiều loại số khác nhau như đã đề cập ở phần trước. Tuy nhiên, có một số loại số đặc biệt trong R cần được nhắc đến.
Số nguyên
Số nguyên là các số không có phần thập phân, ví dụ như 1, 2, 3... Tập hợp số nguyên cũng được coi là một tập hợp con của tập hợp số thực R.
Số thập phân
Số thập phân là các số có phần thập phân, ví dụ như 1.5, 2.75, 3.14159... Tập hợp số thập phân cũng là một tập hợp con của tập hợp số thực R.
Số hữu tỉ
Số hữu tỉ là các số có thể biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên và b không bằng không. Ví dụ, 1/2, 3/4, 7/8... đều là các số hữu tỉ.
Số vô tỉ
Số vô tỉ là các số không thể biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên và b không bằng không. Ví dụ, √2, π, e... đều là các số vô tỉ.
Số dương và số âm
Số dương là các số lớn hơn 0, ví dụ như 1, 2, 3... Trong khi đó, số âm là các số nhỏ hơn 0, ví dụ như -1, -2, -3...
Số không
Số không là số duy nhất trong tập hợp số thực R không thuộc vào bất kỳ loại số nào khác. Nó được ký hiệu là 0 và có tính chất đặc biệt trong các phép tính.
R là tập hợp mở hay đóng?
R là tập hợp số thực mở hay đóng? Đây là một câu hỏi được nhiều người quan tâm khi tìm hiểu về tập hợp số thực. Để trả lời câu hỏi này, chúng ta cần hiểu rõ khái niệm tập hợp mở và tập hợp đóng.
Tập hợp mở
Tập hợp mở là tập hợp có thể được biểu diễn bằng cách sử dụng các điểm bên trong của nó. Ví dụ, tập hợp các số thực từ 0 đến 1 là một tập hợp mở, vì ta có thể biểu diễn nó bằng cách sử dụng các số thực nhỏ hơn 1 và lớn hơn 0.
Tập hợp đóng
Tập hợp đóng là tập hợp có thể được biểu diễn bằng cách sử dụng tất cả các điểm của nó, bao gồm cả các điểm biên. Ví dụ, tập hợp các số thực từ 0 đến 1 kèm theo các số 0 và 1 là một tập hợp đóng, vì ta có thể biểu diễn nó bằng cách sử dụng tất cả các số thực từ 0 đến 1.
R là tập hợp mở hay đóng?
R là tập hợp số thực, do đó nó không thuộc vào bất kỳ loại tập hợp nào trên. Tuy nhiên, ta có thể xem R là một tập hợp đóng vì nó bao gồm tất cả các điểm của nó, bao gồm cả các điểm biên như 0 và 1.
R là tập hợp hữu hạn hay vô hạn?
R là tập hợp số thực, do đó nó là một tập hợp vô hạn. Điều này có nghĩa là tập hợp số thực không có giới hạn về số lượng phần tử, mỗi khi ta thêm một số mới vào tập hợp thì tập hợp vẫn là tập hợp số thực.
R là tập hợp số khả đếm được hay không?
Tập hợp số khả đếm được là tập hợp có thể được liệt kê một cách rõ ràng và có thể đếm được số lượng phần tử của nó. Ví dụ, tập hợp các số nguyên là một tập hợp số khả đếm được vì ta có thể liệt kê từng số nguyên một và đếm được số lượng phần tử của tập hợp này.
Tuy nhiên, tập hợp số thực không phải là tập hợp số khả đếm được. Điều này bởi vì tập hợp số thực chứa cả các số vô tỉ, và các số vô tỉ không thể được biểu diễn bằng cách sử dụng các số nguyên hoặc phân số. Do đó, ta không thể liệt kê và đếm được số lượng phần tử của tập hợp số thực.
R có phải là tập hợp con của tập hợp số phức không?
Tập hợp số phức là tập hợp các số có dạng a + bi, trong đó a và b là các số thực và i là đơn vị ảo. Tập hợp số thực là một trường con của tập hợp số phức, do đó ta có thể nói R là một tập hợp con của tập hợp số phức.
Kết luận
Tập hợp số thực R là một tập hợp rất quan trọng trong toán học và được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Nó bao gồm tất cả các số hữu tỉ và vô tỉ, và có nhiều tính chất đặc biệt như tập hợp đóng và tập hợp vô hạn. Tuy nhiên, R không phải là tập hợp số khả đếm được và cũng không phải là tập hợp con của tập hợp số phức. Việc hiểu rõ về tập hợp số thực R sẽ giúp chúng ta áp dụng nó vào các bài toán và ứng dụng trong thực tế một cách hiệu quả.
Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!

















