Định nghĩa và phân loại bài toán chuyển động
Bài toán chuyển động là những bài toán liên quan đến sự thay đổi vị trí của một vật theo thời gian. Các bài toán chuyển động trong chương trình lớp 5 có thể được phân loại thành các dạng sau:
Chuyển động thẳng đều
Chuyển động thẳng đều là dạng chuyển động mà vật chuyển động với vận tốc không đổi.
Chuyển động thẳng không đều
Chuyển động thẳng không đều là dạng chuyển động mà vật chuyển động với vận tốc thay đổi.
Chuyển động trên dòng nước
Chuyển động trên dòng nước là dạng chuyển động mà vật chuyển động trên một dòng nước chảy với vận tốc xác định.
Chuyển động có sự nghỉ
Chuyển động có sự nghỉ là dạng chuyển động mà vật chuyển động với các khoảng thời gian nghỉ ngơi xen kẽ.
Chuyển động có sự thay đổi vận tốc
Chuyển động có sự thay đổi vận tốc là dạng chuyển động mà vật chuyển động với vận tốc thay đổi theo thời gian.
Đơn vị đo lường trong bài toán chuyển động
Trong các bài toán chuyển động, chúng ta sử dụng các đơn vị đo lường sau:
Quãng đường
Quãng đường là khoảng cách mà vật di chuyển từ điểm xuất phát đến điểm đến. Đơn vị đo lường quãng đường là mét (m).
Thời gian
Thời gian là khoảng thời gian mà vật di chuyển từ điểm xuất phát đến điểm đến. Đơn vị đo lường thời gian là giây (s).
Vận tốc
Vận tốc là tốc độ di chuyển của vật. Đơn vị đo lường vận tốc là mét trên giây (m/s).
Công thức tính quãng đường
Trong các bài toán chuyển động, chúng ta sử dụng công thức sau để tính quãng đường:
Quãng đường = Vận tốc × Thời gian
s = v × t
Trong đó:
- s là quãng đường (m)
- v là vận tốc (m/s)
- t là thời gian (s)
Công thức tính thời gian
Để tính thời gian trong các bài toán chuyển động, chúng ta sử dụng công thức sau:
Thời gian = Quãng đường / Vận tốc
t = s / v
Trong đó:
- t là thời gian (s)
- s là quãng đường (m)
- v là vận tốc (m/s)
Công thức tính vận tốc
Để tính vận tốc trong các bài toán chuyển động, chúng ta sử dụng công thức sau:
Vận tốc = Quãng đường / Thời gian
v = s / t
Trong đó:
- v là vận tốc (m/s)
- s là quãng đường (m)
- t là thời gian (s)
Bài toán chuyển động ngược chiều
Bài toán chuyển động ngược chiều là một dạng bài toán chuyển động thường gặp, trong đó hai vật di chuyển theo hướng ngược chiều nhau.
Ví dụ 1: Hai xe chạy ngược chiều
Một xe ô tô đang chạy với vận tốc 60 km/h. Một xe khác đang chạy ngược chiều với vận tốc 80 km/h. Hỏi hai xe cách nhau bao xa sau 1 giờ?
Để giải bài toán này, chúng ta cần:
- Chuyển đổi đơn vị vận tốc từ km/h sang m/s.
- Vận tốc xe thứ nhất: 60 km/h = 60 × 1000 / 3600 = 16,67 m/s
- Vận tốc xe thứ hai: 80 km/h = 80 × 1000 / 3600 = 22,22 m/s
- Tính tổng vận tốc của hai xe:
- Tổng vận tốc = 16,67 m/s + 22,22 m/s = 38,89 m/s
- Tính quãng đường:
- Quãng đường = Tổng vận tốc × Thời gian
- Quãng đường = 38,89 m/s × 1 h = 38,89 km
Vậy, sau 1 giờ, hai xe cách nhau 38,89 km.
Ví dụ 2: Hai người đi ngược chiều
Một người đang đi bộ với vận tốc 4 m/s. Một người khác đang đi ngược chiều với vận tốc 6 m/s. Hỏi sau bao lâu thì hai người gặp nhau, biết rằng họ cách nhau 200 m lúc ban đầu?
Để giải bài toán này, chúng ta cần:
- Tính tổng vận tốc của hai người:
- Tổng vận tốc = 4 m/s + 6 m/s = 10 m/s
- Tính thời gian:
- Thời gian = Quãng đường / Tổng vận tốc
- Thời gian = 200 m / 10 m/s = 20 s
Vậy, sau 20 giây, hai người sẽ gặp nhau.
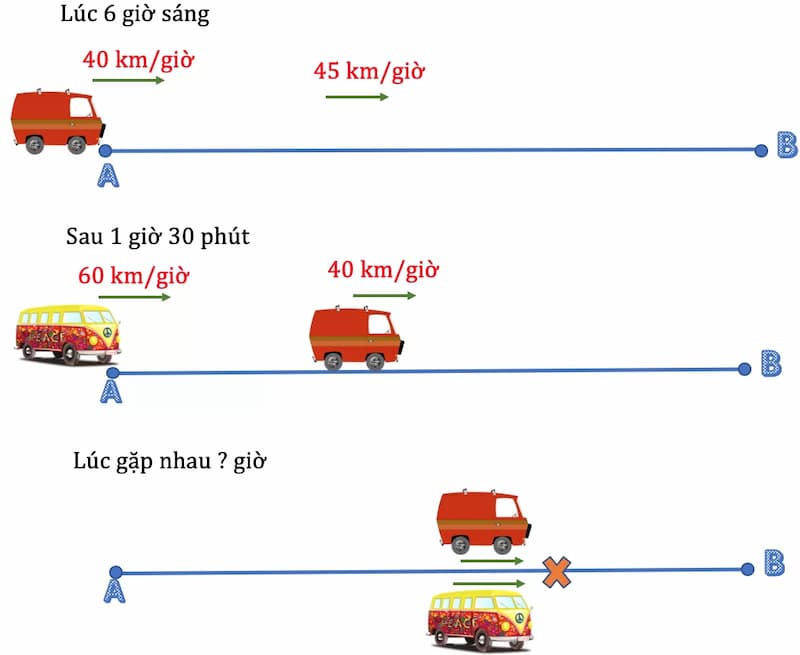
Bài toán chuyển động cùng chiều
Bài toán chuyển động cùng chiều là dạng bài toán chuyển động mà các vật di chuyển theo cùng một hướng.
Ví dụ 1: Hai xe chạy cùng chiều
Một xe ô tô đang chạy với vận tốc 60 km/h. Một xe khác đang chạy cùng chiều với vận tốc 80 km/h. Hỏi sau bao lâu thì xe thứ hai sẽ vượt qua xe thứ nhất, biết rằng lúc đầu cách nhau 5 km?
Để giải bài toán này, chúng ta cần:
- Chuyển đổi đơn vị vận tốc từ km/h sang m/s.
- Vận tốc xe thứ nhất: 60 km/h = 60 × 1000 / 3600 = 16,67 m/s
- Vận tốc xe thứ hai: 80 km/h = 80 × 1000 / 3600 = 22,22 m/s
- Tính vận tốc tương đối của xe thứ hai so với xe thứ nhất:
- Vận tốc tương đối = Vận tốc xe thứ hai - Vận tốc xe thứ nhất
- Vận tốc tương đối = 22,22 m/s - 16,67 m/s = 5,55 m/s
- Tính thời gian:
- Thời gian = Quãng đường / Vận tốc tương đối
- Thời gian = 5 km × 1000 m/km / 5,55 m/s = 900 s = 15 phút
Vậy, sau 15 phút, xe thứ hai sẽ vượt qua xe thứ nhất.
Ví dụ 2: Hai người đi cùng chiều
Một người đang đi bộ với vận tốc 4 m/s. Một người khác đang đi cùng chiều với vận tốc 6 m/s. Hỏi sau bao lâu thì người thứ hai sẽ vượt qua người thứ nhất, biết rằng họ cách nhau 200 m lúc ban đầu?
Để giải bài toán này, chúng ta cần:
- Tính vận tốc tương đối của người thứ hai so với người thứ nhất:
- Vận tốc tương đối = Vận tốc người thứ hai - Vận tốc người thứ nhất
- Vận tốc tương đối = 6 m/s - 4 m/s = 2 m/s
- Tính thời gian:
- Thời gian = Quãng đường / Vận tốc tương đối
- Thời gian = 200 m / 2 m/s = 100 s = 1 phút 40 giây
Vậy, sau 1 phút 40 giây, người thứ hai sẽ vượt qua người thứ nhất.
Bài toán chuyển động trên dòng nước
Bài toán chuyển động trên dòng nước là dạng bài toán chuyển động mà vật di chuyển trên một dòng nước chảy với vận tốc xác định.
Ví dụ 1: Xuồng chạy trên dòng sông
Một chiếc xuồng chạy trên dòng sông với vận tốc 8 m/s theo hướng dòng nước chảy. Dòng sông chảy với vận tốc 2 m/s. Hỏi sau bao lâu thì xuồng sẽ đến được một điểm cách nơi xuất phát 30 km?
Để giải bài toán này, chúng ta cần:
- Tính vận tốc tương đối của xuồng so với bờ:
- Vận tốc tương đối = Vận tốc xuồng + Vận tốc dòng nước
- Vận tốc tương đối = 8 m/s + 2 m/s = 10 m/s
- Tính thời gian:
- Thời gian = Quãng đường / Vận tốc tương đối
- Thời gian = 30 km × 1000 m/km / 10 m/s = 3000 s = 50 phút
Vậy, sau 50 phút, xuồng sẽ đến được điểm cách nơi xuất phát 30 km.
Ví dụ 2: Xuồng chạy ngược dòng
Một chiếc xuồng chạy ngược dòng sông với vận tốc 6 m/s. Dòng sông chảy với vận tốc 2 m/s. Hỏi sau bao lâu thì xuồng sẽ đến được một điểm cách nơi xuất phát 20 km?
Để giải bài toán này, chúng ta cần:
- Tính vận tốc tương đối của xuồng so với bờ:
- Vận tốc tương đối = Vận tốc xuồng - Vận tốc dòng nước
- Vận tốc tương đối = 6 m/s - 2 m/s = 4 m/s
- Tính thời gian:
- Thời gian = Quãng đường / Vận tốc tương đối
- Thời gian = 20 km × 1000 m/km / 4 m/s = 5000 s = 1 giờ 23 phút
Vậy, sau 1 giờ 23 phút, xuồng sẽ đến được điểm cách nơi xuất phát 20 km.
Bài toán chuyển động có sự nghỉ
Bài toán chuyển động có sự nghỉ là dạng bài toán chuyển động mà vật chuyển động với các khoảng thời gian nghỉ ngơi xen kẽ.
Ví dụ 1: Người đi bộ có nghỉ
Một người đi bộ với vận tốc 5 m/s. Sau mỗi 10 phút, anh ta sẽ nghỉ 5 phút. Hỏi sau bao lâu thì người đó sẽ đến được điểm cách nơi xuất phát 3 km?
Để giải bài toán này, chúng ta cần:
- Tính tổng thời gian di chuyển:
- Tổng thời gian di chuyển = Quãng đường / Vận tốc
- Tổng thời gian di chuyển = 3 km × 1000 m/km / 5 m/s = 600 s = 10 phút
- Tính số lần nghỉ:
- Số lần nghỉ = Tổng thời gian di chuyển / (Thời gian đi + Thời gian nghỉ)
- Số lần nghỉ = 10 phút / (10 phút + 5 phút) = 2 lần
- Tính thời gian tổng cộng:
- Thời gian tổng cộng = Tổng thời gian di chuyển + Số lần nghỉ × Thời gian nghỉ
- Thời gian tổng cộng = 10 phút + 2 × 5 phút = 20 phút
Vậy, sau 20 phút, người đó sẽ đến được điểm cách nơi xuất phát 3 km.
Ví dụ 2: Xe ô tô có sự dừng đèn đỏ
Một chiếc xe ô tô chạy với vận tốc 20 m/s. Mỗi khi gặp đèn đỏ, xe sẽ dừng lại trong 30 giây. Hỏi sau bao lâu thì xe sẽ đến được điểm cách nơi xuất phát 5 km, biết rằng có 3 đoạn đường có đèn đỏ?
Để giải bài toán này, chúng ta cần:
- Tính tổng thời gian di chuyển:
- Tổng thời gian di chuyển = Quãng đường / Vận tốc
- Tổng thời gian di chuyển = 5 km × 1000 m/km / 20 m/s = 250 s = 4 phút 10 giây
- Tính thời gian dừng lại:
- Thời gian dừng lại = Số lần dừng × Thời gian dừng
- Thời gian dừng lại = 3 lần × 30 giây = 90 giây = 1 phút 30 giây
- Tính thời gian tổng cộng:
- Thời gian tổng cộng = Tổng thời gian di chuyển + Thời gian dừng lại
- Thời gian tổng cộng = 4 phút 10 giây + 1 phút 30 giây = 5 phút 40 giây
Vậy, sau 5 phút 40 giây, xe sẽ đến được điểm cách nơi xuất phát 5 km.
Bài toán chuyển động có sự thay đổi vận tốc
Bài toán chuyển động có sự thay đổi vận tốc là dạng bài toán chuyển động mà vật chuyển động với vận tốc biến đổi theo thời gian.
Ví dụ 1: Xe máy tăng tốc
Một chiếc xe máy khởi đầu từ vị trí A và tăng tốc đều với gia tốc 2 m/s^2. Biết rằng sau 5 giây, xe đạt vận tốc 10 m/s. Hỏi quãng đường mà xe đã đi được?
Để giải bài toán này, chúng ta cần:
- Tính vận tốc ban đầu của xe:
- Vận tốc ban đầu = Gia tốc × Thời gian
- Vận tốc ban đầu = 2 m/s^2 × 5 s = 10 m/s
- Tính quãng đường:
- Quãng đường = Vận tốc trung bình × Thời gian
- Quãng đường = (Vận tốc ban đầu + Vận tốc cuối) / 2 × Thời gian
- Quãng đường = (10 m/s + 10 m/s) / 2 × 5 s = 50 m
Vậy, quãng đường mà xe đã đi được là 50 mét.
Ví dụ 2: Vật rơi tự do
Một vật rơi tự do từ độ cao 100 mét. Biết rằng vật rơi với gia tốc trọng trường là 9,8 m/s^2. Hỏi sau bao lâu vật sẽ chạm đất?
Để giải bài toán này, chúng ta cần:
- Tính thời gian rơi:
- Thời gian rơi = căn bậc hai(2 × Chiều cao / Gia tốc)
- Thời gian rơi = căn bậc hai(2 × 100 m / 9,8 m/s^2) = 4,52 s
Vậy, sau khoảng 4,52 giây, vật sẽ chạm đất.
Kết luận
Trong bài viết này, chúng ta đã tìm hiểu về bài toán chuyển động và các dạng bài toán phổ biến liên quan đến chuyển động. Để giải các bài toán này, việc áp dụng các công thức tính quãng đường, thời gian, vận tốc và xác định vận tốc tương đối là rất quan trọng. Việc hiểu và áp dụng các kiến thức này sẽ giúp bạn giải quyết các bài toán chuyển động một cách dễ dàng và chính xác. Hy vọng rằng bài viết đã cung cấp cho bạn cái nhìn tổng quan về chủ đề này. Chúc bạn thành công trong việc học tập và giải quyết bài toán!
Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!

















