Giới thiệu về khai triển nhị thức Newton
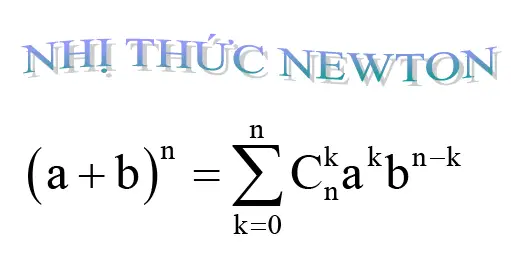
Khai triển nhị thức Newton là một phương pháp toán học được sử dụng để mở rộng một biểu thức bằng cách sử dụng một số công thức đã được xác định trước đó. Phương pháp này được đặt theo tên của nhà toán học Isaac Newton, người đã phát triển và sử dụng nó rộng rãi trong các nghiên cứu của mình.
Khai triển nhị thức Newton được sử dụng rộng rãi trong nhiều lĩnh vực toán học, bao gồm: giải tích, đại số, và các ứng dụng thực tế khác. Phương pháp này cho phép chúng ta tính toán và xác định các số hạng trong một biểu thức, đồng thời cũng giúp chúng ta hiểu rõ hơn về cấu trúc và tính chất của các biểu thức đó.
Các công thức cơ bản
Để có thể tìm các số hạng không chứa x trong khai triển nhị thức Newton, chúng ta cần phải nắm vững các công thức cơ bản sau:
- Công thức khai triển nhị thức Newton: (a + b)n = ∑(n choose k) * a(n-k) * b^k, với k = 0, 1, 2, ..., n
Trong đó:
- a, b là các số hạng trong biểu thức
- n là lũy thừa của biểu thức
- (n choose k) là hệ số phối hợp, được tính bằng công thức: (n choose k) = n! / (k! * (n-k)!)
- Công thức tính hệ số phối hợp: (n choose k) = n! / (k! * (n-k)!)
Trong đó:
- n! là giai thừa của n
- k! là giai thừa của k
- (n-k)! là giai thừa của (n-k)
- Công thức tính giai thừa: n! = 1 2 3 ... n
Trong đó:
- n! là giai thừa của n
- 1, 2, 3, ..., n là các số tự nhiên từ 1 đến n
Với các công thức cơ bản này, chúng ta có thể áp dụng để tìm các số hạng không chứa x trong quá trình khai triển nhị thức Newton.
Áp dụng tìm số hạng không chứa x
Để tìm số hạng không chứa x trong khai triển nhị thức Newton, chúng ta cần phải thực hiện các bước sau:
- Xác định biểu thức cần khai triển:
- Từ biểu thức ban đầu, chúng ta cần xác định các số hạng a và b, cũng như lũy thừa n.
- Áp dụng công thức khai triển nhị thức Newton:
- Sử dụng công thức (a + b)n = ∑(n choose k) * a(n-k) * b^k, với k = 0, 1, 2, ..., n.
- Tính toán các hệ số phối hợp (n choose k) theo công thức tương ứng.
- Xác định các số hạng trong biểu thức khai triển, bao gồm cả số hạng không chứa x.
- Nhận diện số hạng không chứa x:
- Trong quá trình khai triển, chúng ta sẽ tìm được các số hạng không chứa x, tức là các số hạng chỉ chứa các số hạng a hoặc b.
- Số hạng không chứa x sẽ là số hạng có k = 0, tức là a^n * b^0 = a^n.
Bằng cách áp dụng các bước trên, chúng ta có thể tìm được số hạng không chứa x trong quá trình khai triển nhị thức Newton.
Ví dụ minh họa
Để hiểu rõ hơn về cách tìm số hạng không chứa x, chúng ta hãy xem xét một ví dụ cụ thể.
Ví dụ: Hãy tìm số hạng không chứa x trong khai triển nhị thức Newton của (x + 2)^5.
Giải:
- Xác định biểu thức cần khai triển:
- a = x
- b = 2
- n = 5
- Áp dụng công thức khai triển nhị thức Newton: (x + 2)5 = ∑(5 choose k) * x(5-k) * 2^k, với k = 0, 1, 2, 3, 4, 5
Tính các hệ số phối hợp: (5 choose 0) = 1 (5 choose 1) = 5 (5 choose 2) = 10 (5 choose 3) = 10 (5 choose 4) = 5 (5 choose 5) = 1
Thay các giá trị vào công thức: (x + 2)^5 = 1 x^5 2^0 + 5 x^4 2^1 + 10 x^3 2^2 + 10 x^2 2^3 + 5 x^1 2^4 + 1 x^0 2^5
- Nhận diện số hạng không chứa x: Trong biểu thức khai triển, số hạng không chứa x là số hạng có k = 0, tức là x^5 * 2^0 = x^5.
Vậy, số hạng không chứa x trong khai triển nhị thức Newton của (x + 2)^5 là x^5.
Bài tập thực hành
Hãy thực hiện các bài tập sau để củng cố kiến thức về cách tìm số hạng không chứa x trong khai triển nhị thức Newton:
- Tìm số hạng không chứa x trong khai triển nhị thức Newton của (x - 3)^4.
- Tìm số hạng không chứa x trong khai triển nhị thức Newton của (2x + 1)^6.
- Tìm số hạng không chứa x trong khai triển nhị thức Newton của (x^2 + 4)^3.
Hãy áp dụng các bước đã học trong phần trước để tìm ra kết quả chính xác.
Mẹo và lưu ý
Để tìm số hạng không chứa x trong khai triển nhị thức Newton một cách hiệu quả, bạn có thể áp dụng một số mẹo và lưu ý sau:
- Xác định rõ các số hạng a và b: Việc xác định chính xác các số hạng a và b trong biểu thức ban đầu là rất quan trọng. Điều này sẽ giúp bạn áp dụng công thức khai triển nhị thức Newton một cách chính xác.
- Tính toán hệ số phối hợp cẩn thận: Việc tính toán các hệ số phối hợp (n choose k) cũng cần được thực hiện một cách chính xác. Bạn có thể sử dụng công thức hoặc các công cụ tính toán để giảm bớt sai sót.
- Nhận diện số hạng không chứa x: Khi đã có kết quả khai triển nhị thức Newton, hãy tập trung vào các số hạng có k = 0, vì đây chính là số hạng không chứa x.
- Luyện tập thường xuyên: Việc tìm số hạng không chứa x trong khai triển nhị thức Newton cần được luyện tập thường xuyên. Điều này sẽ giúp bạn nắm vững các khái niệm và quen với các bước thực hiện.
- Áp dụng vào các ví dụ khác: Không chỉ dừng lại ở các ví dụ đơn giản, hãy thử áp dụng kỹ thuật này vào các biểu thức phức tạp hơn. Điều này sẽ giúp bạn nâng cao khả năng giải quyết vấn đề.
Với những mẹo và lưu ý trên, bạn sẽ có thể tìm số hạng không chứa x trong khai triển nhị thức Newton một cách hiệu quả hơn.
Ứng dụng trong giải toán
Kỹ thuật tìm số hạng không chứa x trong khai triển nhị thức Newton có nhiều ứng dụng trong việc giải quyết các bài toán toán học. Dưới đây là một số ví dụ về các ứng dụng của kỹ thuật này:
- Giải phương trình và bất phương trình: Khi giải các phương trình hoặc bất phương trình có dạng (a + b)^n = 0 hoặc (a + b)^n ≥ 0, việc tìm số hạng không chứa x sẽ giúp chúng ta xác định được các nghiệm của phương trình hoặc bất phương trình.
- Tính toán xác suất: Trong các bài toán xác suất, khai triển nhị thức Newton được sử dụng để tính toán các xác suất liên quan đến các sự kiện.
- Tính tổng chuỗi: Kỹ thuật này cũng được áp dụng để tính tổng của các chuỗi toán học, đặc biệt là các chuỗi Binomial.
- Ứng dụng trong vật lý và kỹ thuật: Khai triển nhị thức Newton cũng được sử dụng rộng rãi trong các lĩnh vực như vật lý, công nghệ, khoa học máy tính, v.v. để giải quyết các bài toán liên quan.
Bằng cách nắm vững kỹ thuật tìm số hạng không chứa x trong khai triển nhị thức Newton, bạn sẽ có thể áp dụng nó vào việc giải quyết nhiều bài toán toán học và các ứng dụng thực tế khác.
Tham khảo
Để tìm hiểu thêm về khai triển nhị thức Newton và cách tìm số hạng không chứa x, bạn có thể tham khảo các tài liệu sau:
- Sách giáo trình toán học cấp đại học, như "Giải tích Mathematic" của tác giả Nguyễn Đình Trí.
- Các bài viết trên các trang web chuyên về toán học, như "Toán học Việt Nam" (toanhocvietnam.vn) hoặc "Toán học Trường Đại học Khoa học Tự nhiên" (math.hcmus.edu.vn).
- Video bài giảng trên YouTube, chẳng hạn như các video của kênh "Toán học với Hải".
- Các tài liệu tham khảo khác như sách, bài báo khoa học hoặc các nguồn thông tin chuyên ngành liên quan.
Việc tham khảo các nguồn tài liệu đa dạng sẽ giúp bạn hiểu sâu hơn về khai triển nhị thức Newton và các kỹ thuật liên quan.
Kết luận
Trong bài viết này, chúng ta đã tìm hiểu chi tiết về cách tìm số hạng không chứa x trong khai triển nhị thức Newton. Từ việc giới thiệu về khai triển nhị thức Newton, các công thức cơ bản, đến việc áp dụng tìm số hạng không chứa x, cùng với ví dụ minh họa và bài tập thực hành, chúng ta đã có một cái nhìn toàn diện về kỹ thuật này.
Ngoài ra, chúng ta cũng đã tìm hiểu về một số mẹo và lưu ý khi áp dụng kỹ thuật này, cũng như các ứng dụng của nó trong việc giải quyết các bài toán toán học và các ứng dụng thực tế khác.
Hy vọng rằng, thông qua bài viết này, bạn đã nắm vững cách tìm số hạng không chứa x trong khai triển nhị thức Newton và có thể áp dụng nó một cách hiệu quả trong các bài toán toán học cũng như các ứng dụng thực tế khác. Hãy tiếp tục luyện tập và áp dụng kiến thức này để nângcao khả năng giải quyết vấn đề của mình. Chúc bạn thành công trong hành trình học tập và nghiên cứu toán học!
thể áp dụng một số mẹo và lưu ý sau:
- Xác định rõ các số hạng a và b: Việc xác định chính xác các số hạng a và b trong biểu thức ban đầu là rất quan trọng. Điều này sẽ giúp bạn áp dụng công thức khai triển nhị thức Newton một cách chính xác.
- Tính toán hệ số phối hợp cẩn thận: Việc tính toán các hệ số phối hợp (n choose k) cũng cần được thực hiện một cách chính xác. Bạn có thể sử dụng công thức hoặc các công cụ tính toán để giảm bớt sai sót.
- Nhận diện số hạng không chứa x: Khi đã có kết quả khai triển nhị thức Newton, hãy tập trung vào các số hạng có k = 0, vì đây chính là số hạng không chứa x.
- Luyện tập thường xuyên: Việc tìm số hạng không chứa x trong khai triển nhị thức Newton cần được luyện tập thường xuyên. Điều này sẽ giúp bạn nắm vững các khái niệm và quen với các bước thực hiện.
- Áp dụng vào các ví dụ khác: Không chỉ dừng lại ở các ví dụ đơn giản, hãy thử áp dụng kỹ thuật này vào các biểu thức phức tạp hơn. Điều này sẽ giúp bạn nâng cao khả năng giải quyết vấn đề.
Với những mẹo và lưu ý trên, bạn sẽ có thể tìm số hạng không chứa x trong khai triển nhị thức Newton một cách hiệu quả hơn.
Ứng dụng trong giải toán
Kỹ thuật tìm số hạng không chứa x trong khai triển nhị thức Newton có nhiều ứng dụng trong việc giải quyết các bài toán toán học. Dưới đây là một số ví dụ về các ứng dụng của kỹ thuật này:
- Giải phương trình và bất phương trình: Khi giải các phương trình hoặc bất phương trình có dạng (a + b)^n = 0 hoặc (a + b)^n ≥ 0, việc tìm số hạng không chứa x sẽ giúp chúng ta xác định được các nghiệm của phương trình hoặc bất phương trình.
- Tính toán xác suất: Trong các bài toán xác suất, khai triển nhị thức Newton được sử dụng để tính toán các xác suất liên quan đến các sự kiện.
- Tính tổng chuỗi: Kỹ thuật này cũng được áp dụng để tính tổng của các chuỗi toán học, đặc biệt là các chuỗi Binomial.
- Ứng dụng trong vật lý và kỹ thuật: Khai triển nhị thức Newton cũng được sử dụng rộng rãi trong các lĩnh vực như vật lý, công nghệ, khoa học máy tính, v.v. để giải quyết các bài toán liên quan.
Bằng cách nắm vững kỹ thuật tìm số hạng không chứa x trong khai triển nhị thức Newton, bạn sẽ có thể áp dụng nó vào việc giải quyết nhiều bài toán toán học và các ứng dụng thực tế khác.
Tham khảo
Để tìm hiểu thêm về khai triển nhị thức Newton và cách tìm số hạng không chứa x, bạn có thể tham khảo các tài liệu sau:
- Sách giáo trình toán học cấp đại học, như "Giải tích Mathematic" của tác giả Nguyễn Đình Trí.
- Các bài viết trên các trang web chuyên về toán học, như "Toán học Việt Nam" (toanhocvietnam.vn) hoặc "Toán học Trường Đại học Khoa học Tự nhiên" (math.hcmus.edu.vn).
- Video bài giảng trên YouTube, chẳng hạn như các video của kênh "Toán học với Hải".
- Các tài liệu tham khảo khác như sách, bài báo khoa học hoặc các nguồn thông tin chuyên ngành liên quan.
Việc tham khảo các nguồn tài liệu đa dạng sẽ giúp bạn hiểu sâu hơn về khai triển nhị thức Newton và các kỹ thuật liên quan.
Kết luận
Trong bài viết này, chúng ta đã tìm hiểu chi tiết về cách tìm số hạng không chứa x trong khai triển nhị thức Newton. Từ việc giới thiệu về khai triển nhị thức Newton, các công thức cơ bản, đến việc áp dụng tìm số hạng không chứa x, cùng với ví dụ minh họa và bài tập thực hành, chúng ta đã có một cái nhìn toàn diện về kỹ thuật này.
Ngoài ra, chúng ta cũng đã tìm hiểu về một số mẹo và lưu ý khi áp dụng kỹ thuật này, cũng như các ứng dụng của nó trong việc giải quyết các bài toán toán học và các ứng dụng thực tế khác.
Hy vọng rằng, thông qua bài viết này, bạn đã nắm vững cách tìm số hạng không chứa x trong khai triển nhị thức Newton và có thể áp dụng nó một cách hiệu quả trong các bài toán toán học cũng như các ứng dụng thực tế khác. Hãy tiếp tục luyện tập và áp dụng kiến thức này để nâng
Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!

















