Đường trung trực là gì? Tính chất và bài tập về đường trung trực

Đường trung trực là gì?

Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó và đi qua điểm giữa của đoạn thẳng. Nói cách khác, đường trung trực chia đoạn thẳng thành hai phần bằng nhau.

Một số đặc điểm của đường trung trực:

• Đường trung trực vuông góc với đoạn thẳng.
• Đường trung trực đi qua điểm giữa của đoạn thẳng.
• Đường trung trực chia đoạn thẳng thành hai phần bằng nhau.

Ví dụ về đường trung trực

Giả sử chúng ta có một đoạn thẳng AB, với A(x1, y1) và B(x2, y2). Để vẽ đường trung trực của đoạn thẳng AB, chúng ta có thể:

1. Tìm điểm giữa M của đoạn thẳng AB.
2. Vẽ một đường thẳng vuông góc với đoạn thẳng AB và đi qua điểm M.

Đường thẳng vừa vẽ chính là đường trung trực của đoạn thẳng AB.

Tính chất của đường trung trực

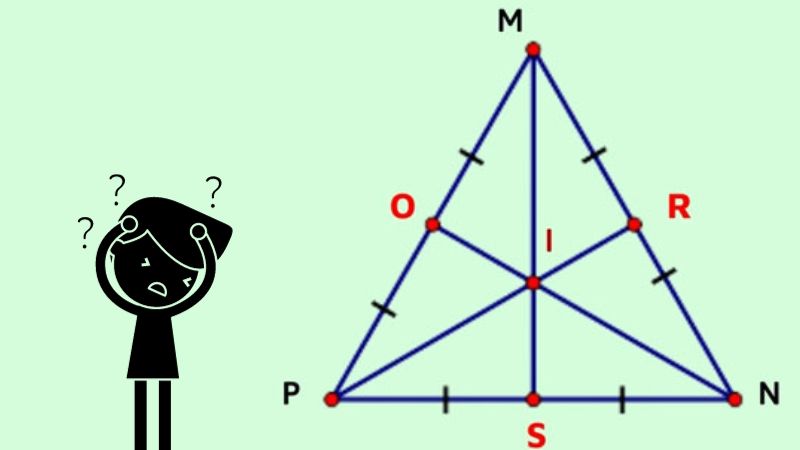
Đường trung trực có nhiều tính chất đặc biệt, sau đây là một số tính chất quan trọng:

1. Đường trung trực chia đoạn thẳng thành hai phần bằng nhau

Như đã nói ở trên, đường trung trực đi qua điểm giữa của đoạn thẳng, do đó nó chia đoạn thẳng thành hai phần bằng nhau.

2. Đường trung trực vuông góc với đoạn thẳng

Đường trung trực luôn vuông góc với đoạn thẳng mà nó chia đôi. Điều này là do định nghĩa của đường trung trực, khi xác định đường trung trực, chúng ta phải vẽ một đường thẳng vuông góc với đoạn thẳng đó.

3. Tất cả các điểm trên đường trung trực đều cách đều hai đầu mút của đoạn thẳng

Vì đường trung trực chia đoạn thẳng thành hai phần bằng nhau, nên tất cả các điểm trên đường trung trực đều cách đều hai đầu mút của đoạn thẳng.

4. Đường trung trực của một đoạn thẳng là đường trung bình của hai đầu mút của đoạn thẳng đó

Điểm giữa của đoạn thẳng được tính bằng công thức: $M = \left(\frac\right)$

Vì đường trung trực đi qua điểm giữa của đoạn thẳng, nên đường trung trực chính là đường trung bình của hai đầu mút của đoạn thẳng.

5. Đường trung trực của một đoạn thẳng là tập hợp tất cả các điểm cách đều hai đầu mút của đoạn thẳng đó

Như đã nói ở trên, tất cả các điểm trên đường trung trực đều cách đều hai đầu mút của đoạn thẳng. Do đó, đường trung trực chính là tập hợp tất cả các điểm cách đều hai đầu mút của đoạn thẳng.

Bài tập về đường trung trực

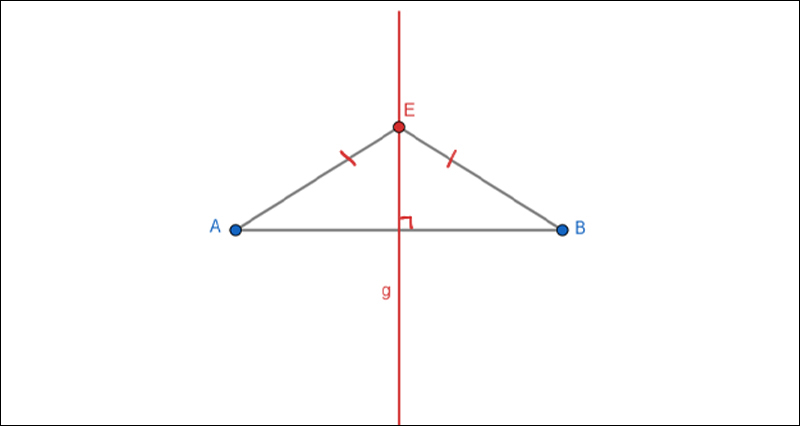
Sau khi tìm hiểu về định nghĩa và tính chất của đường trung trực, chúng ta sẽ xem xét một số bài tập liên quan đến đường trung trực.

Bài tập 1: Vẽ đường trung trực của một đoạn thẳng

Yêu cầu: Vẽ đường trung trực của đoạn thẳng AB, với A(x1, y1) và B(x2, y2).

Giải:

1. Tìm điểm giữa M của đoạn thẳng AB: $M = \left(\frac\right)$
2. Vẽ một đường thẳng vuông góc với đoạn thẳng AB và đi qua điểm M. Đường thẳng vừa vẽ chính là đường trung trực của đoạn thẳng AB.

Bài tập 2: Tìm phương trình đường trung trực của một đoạn thẳng

Yêu cầu: Tìm phương trình đường trung trực của đoạn thẳng AB, với A(x1, y1) và B(x2, y2).

Giải:

1. Tìm điểm giữa M của đoạn thẳng AB: $M = \left(\frac\right)$
2. Tìm hệ số góc của đường thẳng AB: $k = \frac$
3. Tìm hệ số góc của đường trung trực: Vì đường trung trực vuông góc với đoạn thẳng AB, nên hệ số góc của đường trung trực là $k' = -\frac$.
4. Tìm phương trình đường trung trực: Phương trình đường trung trực có dạng: $y - y_M = k'(x - x_M)$ Thay các giá trị tìm được, ta có: $y - \frac)$ Sau khi thu gọn, ta có phương trình đường trung trực: $y = -\frac$

Bài tập 3: Chứng minh ba điểm thẳng hàng

Yêu cầu: Chứng minh rằng ba điểm A(x1, y1), B(x2, y2) và C(x3, y3) thẳng hàng khi và chỉ khi đường trung trực của AB và đường trung trực của AC trùng nhau.

Giải:

1. Giả sử ba điểm A, B, C thẳng hàng.
   • Đường trung trực của AB và AC đều vuông góc với đoạn thẳng AB và AC.
   • Vì ba điểm thẳng hàng, nên điểm giữa của AB và AC trùng nhau.
   • Do đó, đường trung trực của AB và AC trùng nhau.
2. Giả sử đường trung trực của AB và AC trùng nhau.
   • Điểm giữa của AB và AC trùng nhau.
   • Vì ba điểm cùng nằm trên đường trung trực, nên chúng thẳng hàng.

Như vậy, ba điểm A, B, C thẳng hàng khi và chỉ khi đường trung trực của AB và đường trung trực của AC trùng nhau.

Cách vẽ đường trung trực một đoạn thẳng

Để vẽ đường trung trực của một đoạn thẳng, chúng ta có thể sử dụng một trong các phương pháp sau:

Phương pháp 1: Sử dụng compa và thước

1. Đánh dấu hai điểm A và B trên mặt phẳng.
2. Dùng compa đo khoảng cách từ A đến B.
3. Giữ nguyên khoảng cách compa, đặt một chân compa lên điểm A, vẽ một cung tròn. Làm tương tự với điểm B.
4. Đường thẳng đi qua giao điểm của hai cung tròn chính là đường trung trực của đoạn thẳng AB.

Phương pháp 2: Sử dụng phương trình

1. Tìm toạ độ điểm giữa M của đoạn thẳng AB. $M = \left(\frac\right)$
2. Tìm hệ số góc của đường thẳng AB. $k = \frac$
3. Tìm hệ số góc của đường trung trực, vì nó vuông góc với AB. $k' = -\frac$
4. Viết phương trình đường trung trực: $y - y_M = k'(x - x_M)$

Như vậy, bằng cách tìm toạ độ điểm giữa và hệ số góc của đường trung trực, chúng ta có thể viết ra phương trình đường trung trực.

Phương trình đường trung trực đoạn thẳng

Như đã trình bày ở trên, phương trình đường trung trực của một đoạn thẳng AB có dạng:

$y - y_M = k'(x - x_M)$

Trong đó:

• (xM, yM) là toạ độ điểm giữa của đoạn thẳng AB.
• k' là hệ số góc của đường trung trực, được tính bằng $k' = -\frac$.
• Viết phương trình đường trung trực theo dạng $y - y_M = k'(x - x_M)$.

Ví dụ: Tìm phương trình đường trung trực của đoạn thẳng AB, với A(1, 2) và B(4, 5).

Giải:

• 1. Tìm toạ độ điểm giữa M của đoạn thẳng AB: $M = \left(\frac\right) = (2.5, 3.5)$
  2. Tính hệ số góc k của đoạn thẳng AB: $k = \frac = 1$
  3. Tính hệ số góc k' của đường trung trực: $k' = -\frac = -1$
  4. Viết phương trình đường trung trực: $y - 3.5 = -1(x - 2.5)$ Đơn giản hóa, ta có: $y = -x + 6$

Vậy phương trình đường trung trực của đoạn thẳng AB là $y = -x + 6$.

Định lý về đường trung trực

Định lý 1: Ba điểm thẳng hàng khi và chỉ khi đường trung trực của hai trong ba đoạn thẳng tạo bởi ba điểm đó trùng nhau.

Định lý 2: Tất cả các điểm trên đường trung trực của một đoạn thẳng đều cách đều hai đầu mút của đoạn thẳng đó.

Định lý 3: Đường trung trực của một đoạn thẳng là tập hợp tất cả các điểm cách đều hai đầu mút của đoạn thẳng đó.

Định lý 4: Đường trung trực của một đoạn thẳng luôn vuông góc với đoạn thẳng đó.

Định lý 5: Điểm giao của hai đường trung trực của hai đoạn thẳng khác nhau chính là điểm giữa của hai đoạn thẳng đó.

Cách chứng minh ba điểm thẳng hàng

Để chứng minh rằng ba điểm A(x1, y1), B(x2, y2) và C(x3, y3) thẳng hàng, ta có thể sử dụng phương pháp sau:

Bước 1: Sử dụng hình học

• 1. Vẽ đường trung trực của đoạn thẳng AB và AC.
  2. Nếu hai đường trung trực này trùng nhau tại một điểm D, thì ba điểm A, B, C thẳng hàng.
  3. Nếu hai đường trung trực không trùng nhau, thì ba điểm A, B, C không thẳng hàng.

Bước 2: Sử dụng tính chất hệ số góc

• 1. Tính hệ số góc k1 của đoạn thẳng AB và hệ số góc k2 của đoạn thẳng AC.
  2. Nếu k1 = k2, tức là hai đoạn thẳng AB và AC song song, do đó ba điểm A, B, C thẳng hàng.
  3. Nếu k1 ≠ k2, tức là hai đoạn thẳng AB và AC cắt nhau, do đó ba điểm A, B, C không thẳng hàng.

Như vậy, chúng ta có thể chứng minh ba điểm thẳng hàng bằng cách sử dụng định lý về đường trung trực và tính chất hệ số góc của đoạn thẳng.

Bài tập nâng cao về đường trung trực

Bài tập 1:

Cho ba điểm A(1, 2), B(3, 4) và C(5, 6). Hãy chứng minh rằng ba điểm này thẳng hàng bằng cách sử dụng đường trung trực.

Giải:

• • Đầu tiên, ta tính toán được rằng điểm giữa của đoạn thẳng AB là M(2, 3).
  • Hệ số góc của đoạn thẳng AB là k = 1.
  • Hệ số góc của đường trung trực của AB là k' = -1.
  • Viết phương trình đường trung trực của AB: $y - 3 = -1(x - 2)$, hay $y = -x + 5$.
  • Tương tự, ta tính được phương trình đường trung trực của AC là $y = -x + 7$.
  • Do hai đường trung trực trùng nhau tại điểm M(2, 3), nên ba điểm A, B, C thẳng hàng.

Bài tập 2:

Cho ba điểm A(-1, 2), B(2, 0) và C(4, -2). Hãy chứng minh rằng ba điểm này thẳng hàng bằng cách sử dụng tính chất hệ số góc.

Giải:

• • Hệ số góc của đoạn thẳng AB là k1 = -2/3.
  • Hệ số góc của đoạn thẳng AC là k2 = -2/3.
  • Vì k1 = k2, nên ba điểm A, B, C thẳng hàng.

Qua các bài tập nâng cao này, chúng ta có thể áp dụng kiến thức về đường trung trực để chứng minh tính chất của ba điểm thẳng hàng.

Ứng dụng của đường trung trực

Đường trung trực không chỉ đơn giản là một khái niệm trong hình học mà còn được áp dụng rộng rãi trong thực tế. Dưới đây là một số ứng dụng của đường trung trực:

1. Trong kiến trúc

Trong kiến trúc, việc xác định đường trung trực của một đoạn thẳng giúp trong việc xác định vị trí của các cột, dầm, hay các công trình xây dựng khác. Điều này giúp cho việc xây dựng được chính xác và đồng đều.

2. Trong công nghệ

Trong công nghệ, đường trung trực được sử dụng để xác định vị trí của các thiết bị, cảm biến hoặc robot di chuyển. Việc tính toán đường trung trực giúp cải thiện độ chính xác và hiệu suất của các hệ thống tự động.

3. Trong định vị GPS

Trong hệ thống định vị toàn cầu (GPS), nguyên lý của đường trung trực được áp dụng để xác định vị trí chính xác của các điểm trên bản đồ. Các thiết bị GPS tính toán vị trí dựa trên đường trung trực của các tín hiệu từ các vệ tinh.

Với những ứng dụng thực tế như vậy, đường trung trực đóng vai trò quan trọng trong việc giải quyết các vấn đề liên quan đến vị trí và khoảng cách trong không gian.

Những điểm đặc biệt liên quan đến đường trung trực

1. Điểm trung tâm của tam giác

Trong hình học, điểm trung tâm của một tam giác chính là giao điểm của ba đường trung trực của các cạnh của tam giác đó. Điểm trung tâm này có nhiều tính chất đặc biệt và quan trọng trong việc nghiên cứu tam giác.

2. Đường trung trực của một đoạn thẳng vuông góc với đường thẳng đã cho

Nếu ta có một đoạn thẳng và muốn vẽ một đường trung trực của nó sao cho đường trung trực đó vuông góc với một đường thẳng khác đã cho, ta có thể sử dụng tính chất hệ số góc để giải quyết vấn đề này.

3. Đường trung trực của một đoạn thẳng song song với một đường thẳng đã cho

Khi ta cần tìm đường trung trực của một đoạn thẳng sao cho nó song song với một đường thẳng đã cho, ta cũng có thể áp dụng kiến thức về hệ số góc để giải quyết bài toán này.

Những điểm đặc biệt này liên quan chặt chẽ đến đường trung trực và có thể được áp dụng trong nhiều bài toán hình học phức tạp.

Kết luận

Trong bài viết này, chúng ta đã tìm hiểu về đường trung trực, từ khái niệm cơ bản đến các tính chất, phương trình và ứng dụng của nó. Chúng ta cũng đã làm quen với cách vẽ đường trung trực, chứng minh ba điểm thẳng hàng và những điểm đặc biệt liên quan đến đường trung trực. Đường trung trực không chỉ là một khái niệm hình học mà còn có những ứng dụng thực tế quan trọng, giúp chúng ta hiểu rõ hơn về không gian và vị trí trong không gian. Mong rằng bài viết này sẽ giúp bạn hiểu rõ hơn về đường trung trực và áp dụng kiến thức này vào thực tế một cách linh hoạt và hiệu quả.

Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!