Mặt phẳng (Oxy) trong không gian Oxyz
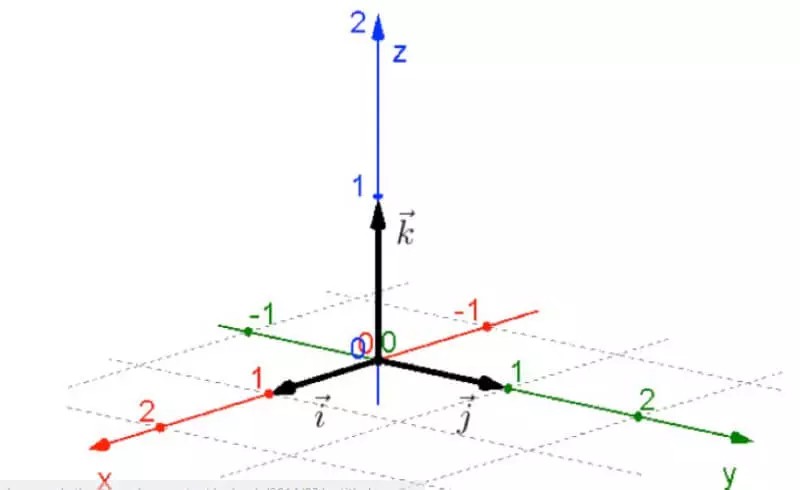
Mặt phẳng (Oxy) là một trong ba mặt phẳng cơ bản trong hệ tọa độ Oxyz. Nó là mặt phẳng được định nghĩa bởi hai trục Ox và Oy, và có phương pháp biểu diễn cũng như tính chất riêng.
Định nghĩa mặt phẳng (Oxy)
Mặt phẳng (Oxy) trong không gian Oxyz được định nghĩa là mặt phẳng được xác định bởi hai trục Ox và Oy, và có phương pháp biểu diễn riêng. Nó là một trong ba mặt phẳng cơ bản của hệ tọa độ Oxyz, cùng với mặt phẳng (Oyz) và mặt phẳng (Ozx).
Phương trình mặt phẳng (Oxy)
Phương trình của mặt phẳng (Oxy) trong không gian Oxyz có dạng:
z = 0
Trong đó, z là tọa độ của điểm trên mặt phẳng (Oxy). Điều này có nghĩa là mặt phẳng (Oxy) là một mặt phẳng nằm trong không gian Oxyz, có tọa độ z bằng 0.
Đặc điểm mặt phẳng (Oxy)
Mặt phẳng (Oxy) có một số đặc điểm nổi bật sau:
- Nằm trong không gian Oxyz: Mặt phẳng (Oxy) là một trong ba mặt phẳng cơ bản của hệ tọa độ Oxyz, cùng với mặt phẳng (Oyz) và mặt phẳng (Ozx).
- Tọa độ z bằng 0: Phương trình của mặt phẳng (Oxy) là z = 0, có nghĩa là tọa độ z của các điểm trên mặt phẳng này luôn bằng 0.
- Chứa các điểm có tọa độ (x, y, 0): Tất cả các điểm có tọa độ (x, y, 0) đều nằm trên mặt phẳng (Oxy).
- Được xác định bởi hai trục Ox và Oy: Mặt phẳng (Oxy) được định nghĩa bởi hai trục Ox và Oy, và có phương pháp biểu diễn riêng.
- Có vai trò quan trọng trong hình học không gian: Mặt phẳng (Oxy) là một trong những mặt phẳng cơ bản và được sử dụng rộng rãi trong nhiều lĩnh vực như toán học, vật lý, kỹ thuật, v.v.
Phương trình mặt phẳng (Oxy) trong không gian Oxyz
Phương trình của mặt phẳng (Oxy) trong không gian Oxyz là một trong những thông tin cơ bản và quan trọng cần được tìm hiểu. Việc hiểu rõ phương trình của mặt phẳng (Oxy) sẽ giúp chúng ta có cái nhìn sâu sắc hơn về tính chất và ứng dụng của nó.
Dạng phương trình mặt phẳng (Oxy)
Như đã đề cập ở trên, phương trình của mặt phẳng (Oxy) trong không gian Oxyz có dạng:
z = 0
Trong đó, z là tọa độ của điểm trên mặt phẳng (Oxy). Điều này có nghĩa là mặt phẳng (Oxy) là một mặt phẳng nằm trong không gian Oxyz, có tọa độ z bằng 0.
Cách biểu diễn phương trình mặt phẳng (Oxy)
Phương trình của mặt phẳng (Oxy) có thể được biểu diễn dưới dạng phương trình tổng quát của mặt phẳng:
Ax + By + Cz + D = 0
Trong đó, A, B, C, D là các hệ số của phương trình. Với mặt phẳng (Oxy), ta có:
A = 0 B = 0 C = 1 D = 0
Vì vậy, phương trình của mặt phẳng (Oxy) có thể được viết dưới dạng:
z = 0
Ý nghĩa của phương trình mặt phẳng (Oxy)
Phương trình z = 0 của mặt phẳng (Oxy) có ý nghĩa rằng tất cả các điểm trên mặt phẳng này đều có tọa độ z bằng 0. Điều này có nghĩa là mặt phẳng (Oxy) nằm ngang và song song với mặt phẳng (Oxy).
Ngoài ra, phương trình z = 0 cũng cho ta thấy rằng mặt phẳng (Oxy) là mặt phẳng cơ bản trong hệ tọa độ Oxyz, cùng với mặt phẳng (Oyz) và mặt phẳng (Ozx).
Định nghĩa mặt phẳng (Oxy) trong không gian Oxyz
Để hiểu rõ hơn về mặt phẳng (Oxy) trong không gian Oxyz, chúng ta cần tìm hiểu về định nghĩa và cách xác định mặt phẳng này.
Khái niệm mặt phẳng (Oxy)
Mặt phẳng (Oxy) là một trong ba mặt phẳng cơ bản trong hệ tọa độ Oxyz, cùng với mặt phẳng (Oyz) và mặt phẳng (Ozx). Nó được định nghĩa là mặt phẳng được xác định bởi hai trục Ox và Oy, và có phương pháp biểu diễn riêng.
Cách xác định mặt phẳng (Oxy)
Để xác định mặt phẳng (Oxy), chúng ta có thể sử dụng các cách sau:
- Dựa trên phương trình: Như đã trình bày ở trên, phương trình của mặt phẳng (Oxy) là z = 0. Tất cả các điểm có tọa độ (x, y, 0) đều nằm trên mặt phẳng (Oxy).
- Dựa trên định nghĩa: Mặt phẳng (Oxy) là mặt phẳng được xác định bởi hai trục Ox và Oy. Nó là một mặt phẳng cơ bản trong hệ tọa độ Oxyz.
- Dựa trên vectơ pháp tuyến: Vectơ pháp tuyến của mặt phẳng (Oxy) là (0, 0, 1). Điều này có nghĩa là mặt phẳng (Oxy) vuông góc với trục Oz.
Bằng cách sử dụng các cách xác định trên, chúng ta có thể dễ dàng xác định và làm việc với mặt phẳng (Oxy) trong không gian Oxyz.
Đặc điểm mặt phẳng (Oxy) trong không gian Oxyz
Mặt phẳng (Oxy) trong không gian Oxyz có một số đặc điểm nổi bật, là những thông tin quan trọng cần được hiểu rõ.
Nằm trong không gian Oxyz
Như đã nói ở trên, mặt phẳng (Oxy) là một trong ba mặt phẳng cơ bản của hệ tọa độ Oxyz, cùng với mặt phẳng (Oyz) và mặt phẳng (Ozx). Nó nằm trong không gian Oxyz và được xác định bởi hai trục Ox và Oy.
Tọa độ z bằng 0
Phương trình của mặt phẳng (Oxy) là z = 0, điều này có nghĩa là tọa độ z của tất cả các điểm trên mặt phẳng này đều bằng 0. Mặt phẳng (Oxy) là một mặt phẳng nằm ngang, song song với mặt phẳng (Oxy).
Chứa các điểm có tọa độ (x, y, 0)
Tất cả các điểm có tọa độ (x, y, 0) đều nằm trên mặt phẳng (Oxy). Điều này có nghĩa là mặt phẳng (Oxy) chứa tất cả các điểm có tọa độ z bằng 0.
Vuông góc với trục Oz
Vectơ pháp tuyến của mặt phẳng (Oxy) là (0, 0, 1), điều này có nghĩa là mặt phẳng (Oxy) vuông góc với trục Oz. Nó được xác định bởi hai trục Ox và Oy, và nằm ngang trong không gian Oxyz.
Vai trò quan trọng trong hình học không gian
Mặt phẳng (Oxy) là một trong những mặt phẳng cơ bản và được sử dụng rộng rãi trong nhiều lĩnh vực như toán học, vật lý, kỹ thuật, v.v. Nó có vai trò quan trọng trong việc mô tả, phân tích và giải quyết các bài toán liên quan đến hình học không gian.
Ứng dụng mặt phẳng (Oxy) trong giải bài toán hình học không gian
Mặt phẳng (Oxy) trong không gian Oxyz có nhiều ứng dụng quan trọng trong việc giải bài toán hình học không gian. Dưới đây là một số ví dụ về ứng dụng của mặt phẳng (Oxy).
Xác định vị trí và hướng trong không gian
Mặt phẳng (Oxy) được sử dụng để xác định vị trí và hướng của các đối tượng trong không gian Oxyz. Ví dụ, khi mô tả vị trí của một điểm trong không gian, ta có thể sử dụng tọa độ (x, y, 0) để chỉ ra rằng điểm đó nằm trên mặt phẳng (Oxy).
Phân tích và mô tả các hình thể trong không gian
Mặt phẳng (Oxy) là một công cụ hữu ích trong việc phân tích và mô tả các hình thể trong không gian. Ví dụ, khi xem xét một hình hộp, ta có thể sử dụng mặt phẳng (Oxy) để mô tả các cạnh, mặt bên và mặt đáy của hình hộp.
Giải bài toán liên quan đến giao của mặt phẳng và các hình thể khác
Mặt phẳng (Oxy) còn được sử dụng để giải các bài toán liên quan đến giao của mặt phẳng với các hình thể khác trong không gian. Ví dụ, tìm đường giao của một mặt phẳng với một đường thẳng hoặc một mặt cầu.
Ứng dụng trong các lĩnh vực khác
Ngoài các ứng dụng trong hình học không gian, mặt phẳng (Oxy) còn được sử dụng rộng rãi trong nhiều lĩnh vực khác như vật lý, kỹ thuật, công nghệ, v.v. Ví dụ, trong vật lý, mặt phẳng (Oxy) được sử dụng để mô tả các hiện tượng liên quan đến chuyển động trong không gian.
Như vậy, mặt phẳng (Oxy) trong không gian Oxyz là một công cụ vô cùng quan trọng và được sử dụng rộng rãi trong nhiều lĩnh vực. Việc hiểu rõ về định nghĩa, phương trình, đặc điểm và ứng dụng của mặt phẳng (Oxy) sẽ giúp chúng ta giải quyết hiệu quả các bài toán hình học không gian.
Ví dụ ứng dụng mặt phẳng (Oxy) trong giải bài toán
Để hiểu rõ hơn về ứng dụng của mặt phẳng (Oxy) trong giải bài toán hình học không gian, chúng ta cùng xem qua một ví dụ cụ thể sau đây:
Ví dụ: Xác định điểm đối xứng qua mặt phẳng (Oxy)
Cho điểm A có tọa độ (2, 3, 4). Hãy xác định điểm đối xứng của điểm A qua mặt phẳng (Oxy).
Giải quyết:
Để xác định điểm đối xứng của điểm A qua mặt phẳng (Oxy), ta sử dụng tính chất của điểm đối xứng qua mặt phẳng. Điểm đối xứng của một điểm A qua mặt phẳng là một điểm B sao cho đoạn thẳng AB vuông góc với mặt phẳng và trung điểm của AB nằm trên mặt phẳng.
Gọi điểm đối xứng của điểm A qua mặt phẳng (Oxy) là B có tọa độ (x', y', z'). Ta có:
- Tọa độ của trung điểm I của đoạn thẳng AB: ((2+x')/2, (3+y')/2, (4+z')/2)
- Vì I nằm trên mặt phẳng (Oxy) nên z' = 0
- Đồng thời, AB vuông góc với mặt phẳng (Oxy) nên vectơ AB song song với vectơ pháp tuyến của mặt phẳng (Oxy), tức là (x'-2, y'-3, z'-4) . (0, 0, 1) = 0
Từ hai điều kiện trên, ta có hệ phương trình:
(x'+2)(0) + (y'+3)(0) + (z'+4)(1) = 0 ⇒ z' + 4 = 0 ⇒ z' = -4
Vậy tọa độ của điểm đối xứng B qua mặt phẳng (Oxy) là (-2, -3, 0).
Qua ví dụ trên, chúng ta đã thấy cách áp dụng mặt phẳng (Oxy) để giải quyết bài toán hình học không gian một cách hiệu quả.
Bài toán cơ bản liên quan đến mặt phẳng (Oxy)
Trong hình học không gian, có nhiều bài toán cơ bản liên quan đến mặt phẳng (Oxy) mà chúng ta có thể gặp phải. Dưới đây là một số bài toán phổ biến:
Bài toán 1: Tìm phương trình mặt phẳng qua ba điểm
Cho ba điểm A, B, C không thẳng hàng trong không gian Oxyz. Hỏi phương trình của mặt phẳng qua ba điểm này là gì?
Bài toán 2: Xác định điểm đối xứng qua mặt phẳng
Cho điểm A và mặt phẳng (Oxy). Hãy xác định điểm đối xứng của điểm A qua mặt phẳng (Oxy).
Bài toán 3: Tìm giao điểm của mặt phẳng và đường thẳng
Cho mặt phẳng (Oxy) và đường thẳng có phương trình trong không gian Oxyz. Hãy xác định điểm giao của mặt phẳng và đường thẳng.
Bài toán 4: Xác định vị trí của điểm trong không gian
Cho điểm M có tọa độ (x, y, z). Hỏi điểm M nằm trên mặt phẳng (Oxy) hay không?
Bài toán 5: Tìm khoảng cách từ một điểm đến mặt phẳng
Cho một điểm P và mặt phẳng (Oxy). Hãy tính khoảng cách từ điểm P đến mặt phẳng (Oxy).
Phương pháp giải bài toán liên quan đến mặt phẳng (Oxy)
Để giải các bài toán liên quan đến mặt phẳng (Oxy) trong không gian Oxyz, chúng ta có thể áp dụng các phương pháp sau:
Sử dụng phương trình mặt phẳng
Khi cần xác định mặt phẳng qua các điểm hoặc tìm giao điểm với mặt phẳng khác, chúng ta có thể sử dụng phương trình của mặt phẳng để giải quyết bài toán.
Sử dụng tính chất của điểm đối xứng qua mặt phẳng
Trong việc xác định điểm đối xứng qua mặt phẳng, chúng ta có thể sử dụng tính chất của điểm đối xứng qua mặt phẳng để tìm ra tọa độ của điểm đó.
Sử dụng vectơ pháp tuyến của mặt phẳng
Vectơ pháp tuyến của mặt phẳng là một công cụ hữu ích để xác định mối quan hệ giữa mặt phẳng và các đối tượng khác trong không gian. Việc sử dụng vectơ pháp tuyến giúp chúng ta hiểu rõ hơn về đặc điểm và ứng dụng của mặt phẳng (Oxy).
Tầm quan trọng mặt phẳng (Oxy) trong hình học không gian
Mặt phẳng (Oxy) không chỉ là một khái niệm cơ bản trong hình học không gian mà còn có tầm quan trọng lớn trong nhiều lĩnh vực khác nhau. Dưới đây là một số điểm quan trọng về tầm quan trọng của mặt phẳng (Oxy):
- Mặt phẳng (Oxy) giúp xác định vị trí và hướng của các đối tượng trong không gian.
- Nó là công cụ quan trọng trong việc phân tích và mô tả các hình thể trong không gian.
- Mặt phẳng (Oxy) được sử dụng rộng rãi trong giải các bài toán hình học không gian.
- Nó có vai trò quan trọng trong việc mô tả các hiện tượng và quy luật trong vật lý và các lĩnh vực khác.
Với những vai trò và ứng dụng đa dạng, mặt phẳng (Oxy) đóng vai trò quan trọng trong việc nghiên cứu và áp dụng trong thực tiễn.
Mở rộng khái niệm mặt phẳng (Oxy)
Ngoài mặt phẳng (Oxy) trong không gian Oxyz, chúng ta cũng có thể mở rộng khái niệm mặt phẳng đến không gian ba chiều khác. Cụ thể, mặt phẳng (Oxy) có thể được mở rộng sang không gian bốn chiều, năm chiều, v.v. để nghiên cứu và áp dụng trong các lĩnh vực phức tạp hơn.
Việc mở rộng khái niệm mặt phẳng giúp chúng ta hiểu rõ hơn về tính chất và đặc điểm của không gian nhiều chiều, từ đó áp dụng vào các bài toán thực tế có tính phức tạp cao.
Kết luận
Trong bài viết này, chúng ta đã tìm hiểu về mặt phẳng (Oxy) trong không gian Oxyz, từ định nghĩa, phương trình, đặc điểm, ứng dụng cho đến các bài toán và phương pháp giải quyết liên quan. Mặt phẳng (Oxy) không chỉ là một khái niệm cơ bản mà còn có tầm quan trọng lớn trong hình học không gian và các lĩnh vực khác. Việc hiểu rõ về mặt phẳng (Oxy) giúp chúng ta áp dụng kiến thức vào thực tiễn một cách hiệu quả và sáng tạo.
Mọi thắc mắc quý khách hàng xin vui lòng gửi về số Hotline 1900.868644 hoặc địa chỉ email [email protected] để được giải đáp. Trân trọng!

















